Rudolf Kaehr Dr.phil@
Copyright ThinkArt Lab ISSN 2041-4358
Abstract
Speculations about trans-functorial and morphic metamorphosis of space - time and worlds on one side, and flux and charge of electronics on the other side, leading to the memristor and memristive systems of nanoelectronics.
Achievements and attempts to surpass classical paradigms of science by Gotthard Gunther and Leon O. Chua are portrayed and other attempts of Robert Rosen’s anticipatory systems are sketched and Martin Heidegger’s late philosophy of the Fourfold are mentioned. Not yet sketched are other theories of the magic of four by Carl Gustaf Jung and Kent D. Palmer’s quadralectics.
Glasgow, 19.02.2010, with some complementation 13.08.2011
The physical and informatic interpretation of bifunctoriality or the other way round, the interpretations of physical and informatic structures and processes as bifunctorial are strictly separating their conceptual categories. Bifunctoriality holds between composition and juxtaposition, only. There is no queerness involved. This is in a healthy correspondence to the presupposed paradigm of rationality, logic and mathematics.
But there are immanently other possibilities too. As proposed, the transversal and the orthogonal interpretation of the interactionality of composition and juxtapositions allows possibilities beyond the healthiness of the established implementations.
Gotthard Gunther has speculated in the ‘50s about a transformation of space and time.
Even with the bifunctorial interpretation of quantum physics, this is still a cranky phantasy. Again, the distinction between composition and juxtaposition is strict and bifunctoriality is showing very well its strict separation. If composition is correlated to sequentiality, i.e. time, and juxtaposition with spatiality, i.e. space, an interchange of space and time is definitively excluded. No time process inverses into a spatial event or state, nor is any spatial event metamorphosing itself into a time-event.
But that’s exactly what we need!
Transversality, laterality and orthogonality of diamondal ‘bifunctoriality’ is doing the job.
How to realize inter-stellar travel?
"Asimov like many other science fiction writers sees quite clearly that the possibility of space-travel depends on the elimination of spatial distance.
The question, therefore, is: Will it be possible to devise a technique of locomotion where we "jump," as Asimov says. In other words:
Where we do not pass space-quants when we cover distance.” (Gunther)
Isaac Asimov, The Stars, Like Dust. N.Y., 1951 (Doubleday), pp.39/40
Following an invitation by the cybernetician Warren McCulloch Gunther to join the Biological Computer Laboratory, Urbana, Illinois as a research professor, Gunther didn’t continue his speculations published in John Campbell’s science fiction magazine “Astounding Stories”. Later Campbell published an interesting paper about Gunther’s new theories in his new journal “analog”, science fact & science fiction vol. LXXI, No. 6, August 1963, pp. 6, 92-94.
http://www.vordenker.de/gunther_web/subconscious.htm
What followed had been profound studies about the inter-relationship of time and logic in the framework of his place-valued logics and morphogrammatics. With that, he was far beyond Heidegger’s “Sein und Zeit" (Being and Time) and ”Time and Being”. But unfortunatetly he didn’t directly continue his post-academic speculations.
Asimov’s ultimate jump: “It is only the Jump which makes interstellar travel possible."
"No matter how good our travel methods might become, there is always a critical point where the accumulated number of space-quants becomes too much for our operational methods. The question, therefore, is: Will it be possible to devise a technique of locomotion where we "jump," as Asimov says.
In other words: Where we do not pass space-quants when we cover distance."
Preparing the construction
(3) The Michelson-Morley experiment implies that absolute Space and absolute Time are abstract relations but not physical realities.
(4)The quantum field theory informs us, that the basic substratum of all physical existence are a limited number of quantum fields, each with the characteristic of extending over all of Space and through all of Time.
We have not yet reached the stars, because we use an extremely limited operational procedure for locomotion - a general procedure, by the way, which includes everything from the crawling of a toddler to the flight of a jet plane or a rocket.
Our question is: Is there a basically different type of operational method? A method more adequate to traverse cosmic distances? The answer is Yes, and it is implied by arguments (3) and (4).
So far we have obtained two very important results! If we use spatial distance (S) as a basis, we obtain an interchange-relation
T << M (1)
If matter (M) is considered to be the constant we find that
S << T (2)
holds. Having arrived at this point we can no more evade the question: Is there a third interchange-relation where (T) is the basic constant? My answer is a very positive Yes. There must be a third exchange-relation
M << S (3)
because the mutual interdependence of (S), (M) and (T) is such that the first two interchange relations could never exist unless a third between (M) and (S) would balance them.
Interchange-relation (3) is the most interesting for us. We know (1) only to the limited extent of our daily experience in terrestrial travel. (2) Is at the moment a purely metric problem between the two continua Space and Time. But (3) represents the very core of modern quantum-mechanical physics.
Only a "little" question is now left. How can we develop a technique of locomotion which does no more use Space in its quantized material aspect, but which utilizes Matter in its, non-quantized spatial version?
Interchangeability of time, space and matter.
"That is the reason why we cannot be satisfied that science, as it is known today, recognizes only three parameters of the Real:
the objective parameter : Matter (M);
the dimensional parameter : Space (S);
the relational parameter : Time (T).
It is necessary to add a fourth cosmical component: the operational parameter: Process (P).
As long as we refuse to accept P as an independent parameter we can only build a technique based on the natural laws inherent in the relations between M, S and T. In this case we will never reach the stars.”
"Thus - introducing P for ![]() and
and ![]() - we have now four equally fundamental parameters: P-M-S-T."
- we have now four equally fundamental parameters: P-M-S-T."
"Everything that exists has three, components. The three natural components of the Universe are M, S and T. But if Man introduces an artificial state of existence he likewise needs three components only. But, being artificial, this state of existence is based on an operation "op" - which, in its turn, acts as a basic component.
"This science can never provide us with an adequate theory of interstellar space-flight because the distributed P cannot absorb the quantized character of M. And nothing can be done about it because, in a MST-universe P can never be taken out of its distribution. Why not? Well, according to our traditional ideas Matter is Something and empty Space and eventless Time are Nothing.
But what is Process (P)? A very embarrassing question! It certainly is nothing!
But is it a thing? No, we cannot admit that either. The science we know uses a strictly two-valued logic. In other words, there can be no basic Third between Something and Nothing. In this system there is no room for an independent P. Consequently the only method to, find an asylum for the fourth parameter was its distribution over the other components."
"The recognition of Process (P) as a new parameter beside Matter, Space and Time is equivalent to introducing in experiential terms that so-much-talked-about "fourth-dimension", through which the first three can be rotated at will. This method permits the substitution of the properties of one parameter by those of the three others. The development of a physical science which satisfies these conditions is now only a question of time. And when this time arrives - "Why, the stars are as near as we wish them."
Gotthard Gunther: Achilles And the Tortoise, part 3 of 3, September 1954
Astounding Science Fiction, September 1954
Editors: John W. Campbell, Jr.
http://www.isfdb.org/cgi-bin/pl.cgi?57679+c
![[Graphics:HTMLFiles/Power of Four_3.gif]](../../Memristics/Power of Four/HTMLFiles/Power of Four_3.gif)
Cover: Frank Kelly Freas, Astounding Science Fiction
http://www.kellyfreas.com
http://www.vordenker.de/gunther_web/achill3.htm
There are rumors about the picture. Is it after Gotthard Gunther?
Trans-monoidal category and ontology
It is proposed by my own speculations that transversality, laterality and orthogonality might offer a first step to formalize this crazy speculation of a transformation of time into space and space into time as a process P of metamorphosis.
Asimov’s Jump is just a first step in the change of the classical paradigm towards metamorphosis. A jump leaves the territory for another place. Metamorphosis is both at once: departure and arrival, i.e. change and preservation together.
Hence, in such an augmented reality, the concept of matter in time- and space-relations becomes a highly contextu(r)al matter.

Bifunctorialty: interaction between time and space, interactional
Transversality: process (P), i.e. metamorphosis of matter between time and space, operational.
Thus, Gunther’s approach is augmenting reality from the M-S-T-structure by the operationality of the process P, to a M-S-T-P structure, but is not yet considering the interaction between space and time in terms of bifunctoriality. The conceptual status of the interactions is missing or is moved to the idea of a 3-valued logic and a replacement of ”ontological” semantics of logical values, true and false, to a non-ontological thematization of meontics (greek: me on = non being, christian: Theory of Evil). Hence, the operationality of P is holding in a non-ontological realm but still restricted to a single universe and excluding therefore the metamorphic aspects of P, i.e. the transversality of a metamorphosis between different worlds.
What has to be achieved is not only to study the interaction between sequential and parallel processes, i.e. composition and juxtaposition, but additionally, the exchange of the terms, representing as objects matter, between composition and juxtaposition. That is, temporal terms are becoming spatial terms, and vice versa, spatial terms are becoming temporal terms. This queer process between composition and juxtaposition, i.e. ‘time’ and ‘space’, is ruled by the features of transversality and orthogonality of metamorphosis. Obviously, this process of metamorphosis is, as such, neither spatial nor temporal.
Without doubt, such a metamorphical ontology is not in harmony with the Western paradigm of thinking the world in the mode of identity of objects and processes.
Personally, this part of Gunther’s speculations was for a longtime not accessible to my understanding. The first understanding I got was in the context of my conceptual studies of Chua’s memristor as a Fourth Element, and after that as its generalization to the idea of memristive systems.
With hindsight it turned out that my speculations about a diamond category theory is just the missing link for a possible understanding of Gunther’s fourth principle. Later on, I modeled memristivity along diamond category theory and morphogrammatics but didn’t came across Gunther’s cosmological speculations again.
How is Gunther’s construction to understand logically? The logical implication involved in the relation “<<" seems not to be transitive.
If T << M and S << T then M << S.
The formula S << T<< M --> M << S is obviously contradicting logical transitivity, i.e. S << T<< M --> S << M.
This is not an accidental situation, Gunther started a similar a-logical construction many years before he had to emigrate to the USA and had to choose SiFi magazines to publish his ideas. Without surprise, the academic journals for philosophy and metaphysics didn’t accept his papers.
The paper, proposed at IX Congress of Philosophy, Paris, and published 1937 develops a new paradigm of philosophy with an intransitivity between time, thought and will. This paper is a short systematizations of even earlier philosophical speculations of Gunther.
"Denn wie man unmittelbar sieht, können auf Grund der drei Prinzipien :
1) Die Zeit ist von höherer Mächtigkeit als der Wille.
2) Das Denken besitzt höhere Mächtigkeit als die Zeit.
3) Der Wille entwickelt eine höhere Mächtigkeit als das Denken,
niemals drei Aussagegruppen von transitivem Charakter gebildet werden. Folglich lässt sich das Zeitproblem auch nicht auf das unmittelbare Verhältnis von Handeln und Denken reduzieren und in ihm auflösen. Auf Grund der mangelnden Transitivität der drei Prinzipien bleibt der Zeitverlauf im konkreten Bewusstsein stets doppelsinnig, und um dem Problem der Metaphysik der Geschichte gerecht zu werden, bedarf die Philosophie deshalb noch einer dritten Transzendentalwissenschaft, die den zeitlichen Horizont des existenten Selbstbewusstseins als geschichtliches Dasein beschreibt.”
Gotthard Günther, Wahrheit, Wirklichkeit und Zeit, die transzendentalen Bedingungen einer Metaphysik der Geschichte. in: Travaux du IXe Congès International de Philosophie, Paris, 1937, p.105-113.
Reprinted in: Gotthard Günther, Beiträge zur Grundlegung einer operationsfähigen Dialektik, Bd. I, Felix Meiner, Hamburg 1976, p.1-8.
Hence, Gunther’s “Denkfigur” states:
time > will and thinking > time and will > thinking.
Thus, thinking > time > will => will > thinking.
Formally, A --> B ![]() B --> C => C --> A.
B --> C => C --> A.
From the point of view of implicational logic, this is strictly false. Worse, such an application of implications on terms like time, will, thought or time, matter, space is utterly nonsensical. First of all because such terms are not propositions. Modelled by sets as categories for an Aristotelian term logic, things are not better.
But who says that Gunther is applying implicational or propositional logic at all?
In later papers following the speculations about the “Fourth Dimension” a the process P Gunther introduces his place-valued logic in which implications are distributed over different loci enabling a system of linear and circular entailments.
This trend of thinking culminated at the end of his life in a theory of negation cycles of all sorts and a theory of “negative languages” in contrast to the positive languages of classical logic and anglo-saxon analytical philosophy and science.
Therefore we might speculate that Gunther’s speculations might be reformulated and brought to some intelligibility by an application of the late formalisms on the idea of a process as the Fourth Dimension.
Another modeling inherent of Gunther’s speculation is opened up by his “context-valued logics”.
Instead of an external description of the triadic structure (M, T, S), this triadic constellation might by contextualized by an internal modeling of the structure from each of its constituents. Such an internal modeling and the changes from one point of view to another for modeling the triadic structure gives the structure some kind of dynamics. This kind of dynamics of the process of constituting the triadic structure might be understood as the fourth dimension, i.e. the prossesuality of the process P.
"The recognition of Process (P) as a new parameter beside Matter, Space and Time is equivalent to introducing in experiential terms that so-much-talked-about "fourth-dimension", through which the first three can be rotated at will.”
The idea, that the process P is understood as the fourth dimension might be misleading. If it suggests that there is anything beyond the triple (M, S, T) then it must be one of the constituents M, S or T. But it is stipulated that the 3 constituents M, S, T are defining the whole “universe”.
Therefore, the interpretation of the process P as an “environment” of the triad doesn’t mean that the environment is of the kind of M, S, T.
The process of the change of interpretation of the triad from one to another position of interpretation, which is in fact a kind of a self-interpretation, doesn’t require a new metaphysical function or entity, but is covered by the concept of the processuality of the changes as such, therefore it is reasonable to interpret such changes as immanent character of the process P.
In other words, the contextual self-constitution of the triadic structure (M, S, T) by the change of the positions of constitution shall be interpreted as the ‘invisible’ and hidden processuality of the process P.
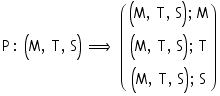
"Of course, P is also present in these three formulas, but as I remarked before, it is distributed over the other parameters, and, therefore, has no quotable value as an independent component. This situation is unavoidable, in classical science.” (Gunther)
Despite some European latecomer, the project of advanced space travel has moved from the USA to China. We might ask: Are the Chinese prepared for a new epoch in space travelling? Or is there anybody else able to enter the new epoch of interstellar travels?
Space travel up to now is still a question of ballistics. How to shoot and transport an object from A to B, here, from a place A on earth to a place beyond the topography of the earth to an extra-planetarian area. This question of transportation was well solved with the visit to the moon, followed by attempts to reach the mars. All based on classical methods and techniques of ballistic physics.
Interestingly, there are not many ideas even in science fiction today which are surpassing speculatively the limitations of the basic principles of modern physics - ballistics, relativity or quantum.
An Aperçu from my blog The Chinese Challenge, SATURDAY, JULY 14, 2007
Chinese ontology (cosmology) can be put into two main statements:
A. Everything in the world is changing.
B. The world, in which everything is changing, doesn't change.
This two main statements are designing a paradoxical constellation.
Hence,
1. The finiteness of the world is not closed but open.
Because of the changing statement (A) the finiteness (B) is not static.
"In a closed world, which consists of many worlds, there is no narrowness. In such a world, which is open and closed at once, there is profoundness of reflection and broadness of interaction." (The Book of Diamonds, Intro)
2. Everything in the world is connectable.
Because of the finite structure of the world, entities are accessible in many ways.
3. Connections are bi-directional.
Because of the finiteness there is no uni-directionality in linear time.
4. Bi-directionality is chiastic.
Because the world is changing, the way back is not exactly the same as the way forwards. This is defining the heterarchic grid structure of the world.
5. The modeling process of Chinese ontology is not phono-logocentric.
Because of the paradoxical character of the "ontology" it can not be represented by phono-logical statements of identity-based mathematics and logic.
Therefore,
6. Because it is written in logical sentences, this aperçu of a definition of Chinese ontology is a paradox metaphor.
7. A first operative description and formalization of Chinese ontology is proposed by the Diamond Theory, which is in a trans-phonological sense a paradox.
8. Diamond theoretic paradox is positively inscribed in Diamond Theory as the interplay, i.e., chiasm, between categories and saltatories. Saltatories are complementary to categories. Complementarity is not duality.
9. The structure of the interplay (chiasm) of categories and saltatories in Diamond Theory is defined by the proemial relationship.
10. The proemiality of the proemial relationship is inscribed as an interplay between order-, exchange- and coincidence relations, distributed over different loci.
11. Because of the finiteness of the world, Diamonds have a location in it. The location (position) of Diamonds is inscribed by their place-designators.
Thus,
12. The self-referential paradoxy/parallaxy of the metaphor of Chinese ontology is realized by the operative calculus of Diamonds as an interplay between categories and saltatories of Diamond Theory.
http://www.thinkartlab.com/CCR/2007/07/chinese-ontology.html
The Chinese Challenge
http://www.docin.com/p-49522764.html
According to the 2 main characteristics of Chinese ontology the missing feature is obvious: There is no change of worlds from one world to another world. Every change is restricted to one and only one world only.
A. Everything in the world is changing.
B. The world, in which everything is changing, doesn't change.
Hence, a fourfold cosmology has to be radicalized to a many-world metamorphosis:
C. The world in which everything is changing is changing too.
D. Worlds are changing by metamorphical transformations of worlds into worlds and ‘objects’ in worlds.
"In a closed world, which consists of many worlds, there is no narrowness. In such a world, which is open and closed at once, there is profoundness of reflection and broadness of interaction. In such a world, it is reasonable to conceive any movement as coupled with its counter-movement."
http://rudys-diamond-strategies.blogspot.com/2007_06_01_archive.html
Space and time are considered as bifunctorial. And bifunctoriality is neither time nor space.
Such a bifunctorial understanding of the interchange of time and space as space/time belongs to a closed world-view. Time and space might interchange but nothing new will happen with and within time and space. Whatever they are they remain what they are in this interchange relation. It would catastophically disturb this world-view if something like a metamorphosis would happen.
I certainly don’t proclaim any seriousness of my diamond formula for the process of metamorphosis of cosmological space and time, transforming matter. Nevertheless, this diamond formula seems to be quite close to the reasonability of the established bifunctorial formula, proposed for the interaction of time and space.
As we know from other studies, metamorphosis is not working within the paradigm of is-abstractions, but demands for as-abstractions of its terms. Terms in quantum physics are not “atomistic”, a fact that is not reflected in the categorical approach, where terms appear as objects of morphisms. Terms in a polycontextural framework are results of interpretations of thematizations, hence the as-abstraction. That is, instead of the term identity A = B of an is-abstraction has to be transformed to the formula ‘A as C corresponds B as D’. The following citation might give a hint for an understanding of the as-abstraction in quantum physics.
"Modern quantum mechanics put an end to atomism and hence to reductionism: The so-called “elementary particles” (such as electrons, quarks, or gluons) are patterns of reality, not building blocks of reality. They are not primary, but arise as secondary manifestations, for example as field excitations, in the same sense as solitons are localized excitations of water, and not building blocks of water.” Hans Primas, Mind & Matter Vol. 5(1), pp. 7-44, 2007
⊗ )/( g _ 2))
" width="562" height="207"/>
From bifunctoriality to laterality (transversality)
Coecke’s sentence for par/seq-inter-functorality :
"We read this as: since f1 is causally before g1 and f2 is causally befor g2, the pair (f1, f2) is causally before (g1, g2) and vice versa [...]."
might be rephrased for transversality/seq (=transversality):
We read this as: since f1is causally before g![]() and f2 is causally before g1, the pair (f1, f2) is causally before cross-pair (g2, g1) and vice versa, i.e. since the pair (f1, f2) is causally before the cross-pair (g2, g1), f1is causally before g2 and f
and f2 is causally before g1, the pair (f1, f2) is causally before cross-pair (g2, g1) and vice versa, i.e. since the pair (f1, f2) is causally before the cross-pair (g2, g1), f1is causally before g2 and f![]() is causally before g1.
is causally before g1.
and additionally,
we will complete the scheme with the transversality/par (=diagonality) interpretation :
We read this as: since f1is causally before gand f2 is causally before g1, the pair (f1, g1) is causally before the pair (f2, g2) and vice versa, i.e. since the pair (f1, g1) is causally before the pair (f2, g2), f1is causally before g2 and f![]() is causally before g1.
is causally before g1.

Wording
f1 as f![]() f1≡f
f1≡f![]() is connected with g1as g1, g1≡g1, by composition :
is connected with g1as g1, g1≡g1, by composition : ![]()
f2 as f2, f2≡f![]() is connected with g2 as g2, g1≡g1, by composition :
is connected with g2 as g2, g1≡g1, by composition : ![]()
f1 as f1 is connected with f2 as f2 by juxtaposition :
g1 as g1 is connected with g2 as g2 by juxtaposition : ![]()
f1 as f'1, ![]() , is connected with g2 as g'2 ,
, is connected with g2 as g'2 , ![]() , by transversality :
, by transversality : ![]()
g1 as g'1, ![]() , is connected with f2 as f2,
, is connected with f2 as f2, ![]() , by transversality :
, by transversality : ![]()
Hence, the term “f” as "(f, f’)" is at once
in a compositional relation with “g”
and in a transversal relation with “g’” ,
as well as in a juxtapositional relation with the composition “o".

The common of all interchanges of space and time is the pre-given world in which this interchange happens. This is loyal the the principle: “Everyting in this world is changing. The world in which everything is changing is not itself changing.”
Morphic metamorphosis is opting for a multitude of worlds. Hence, interchange happens in a double way: between different worlds and inside a world.
This opens up the possibility that one space/time event might interchange not in itself but between its world and a discontexturally different world.
It seems as a main restriction of the Chinese dynamical cosmology that it is restricted to change immanently in a world and not between different worlds. Change between different worlds is demanding for more than a monolithic concept of harmony.
A similar idea of polycontextural change occurs much later in Gunther’s Moscow lecture (1970) as the “The Historical Category of the New” using a mechanism of symmetry/asymmetry and elementary/compound contextures.
http://www.vordenker.de/ggphilosophy/gg_category.pdf
The question of distance becomes obsolete in the process of morphic metamorphosis of the interplay between/with space-time and one/many worlds.
How are worlds appearing?
Space and time are not contained in a world but the world of a space/time-interchange appears as the meta-system of both, i.e. as the diamond environment, short, as the saltatory of the categorical reality of the interchanging time and space.
At first, the formula seems to be too close to the mono-contextural interchangeability of space and time.
Gunther’s fourth category, process, is “invisible”, it is in fact the condition of the possibility of both, the in-world space-time-matter constellation.
In the same way, worlds are invisible to in-world possibilities of space-time-matter configurations.
"The recognition of Process (P) as a new parameter beside Matter, Space and Time is equivalent to introducing in experiential terms that so-much-talked-about "fourth-dimension", through which the first three can be rotated at will.”
"According to classical principles the phenomenon in question is based on the formulas.
S / M = T,
S / T = M,
M T = S.
These are expressions of basic laws in a three-parameter-universe (MST).
Of course, P is also present in these three formulas, but as I remarked before, it is distributed over the other parameters, and, therefore, has no quotable value as an independent component. This situation is unavoidable, in classical science.”
What’s the matter with “matter”?
”...neither Space nor Time are absolute data of our scientific experience, and that they exist only in an interdependent relation with Matter. But so far we have not yet discussed Matter.” (Gunther)
Matter is relative, it might be the formal “objects” of a structural formula, it will change between temporal matter and spacial matter. As much as time and space are functions of matter too.
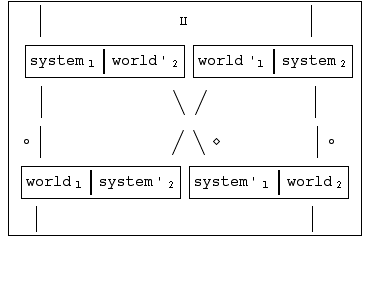
Structure of structural coupling of ... nbsp; : in - world
" width="582" height="281"/>
From Universe to Polyverses
http://memristors.memristics.com/Polyverses/Polyverses.pdf
Who says we are doing physics, and who says the physicians are not doing metaphysics?
Leon Ong Chua (Chinese: 蔡少堂; born June 28, 1936) studying electronics, surrounded by his wife and four daughters, didn’t feel comfortable with "The holy trinity: resistors, inductors and capacitors, are three and one at the same time.” (Nicolau Warneck)
http://current.com/154264c
"But the hypothetical device was mostly written off as a mathematical dalliance.”
"Electronic theorists have been using the wrong pair of variables all these years--voltage and charge. The missing part of electronic theory was that the fundamental pair of variables is flux and charge," said Chua.
"The situation is analogous to what is called Aristotle's Law of Motion, which was wrong, because he said that force must be proportional to velocity.
That misled people for 2000 years until Newton came along and pointed out that Aristotle was using the wrong variables. Newton said that force is proportional to acceleration--the change in velocity. This is exactly the situation with electronic circuit theory today. All electronic textbooks have been teaching using the wrong variables--voltage and charge--explaining away inaccuracies as anomalies. What they should have been teaching is the relationship between changes in voltage, or flux, and charge.”
http://arstechnica.com/civis/viewtopic.php?f=26&t=117871
LEON 0. CHUA, Memristor-The Missing Circuit Element
"This paper presents the logical and scientific basis for the existence of a new two-terminal circuit element called the memristor (contraction for memory resistor) which has every right to be as basic as the three classical circuit elements already in existence, namely, the resistor, inductor, and capacitor.
Although the existence of a memristor in the form of a physical device without internal power supply has not yet been discovered, its laboratory realization in the form of active circuits will be presented in Section II.”
"From the logical as well as axiomatic points of view, it is necessary for the sake of completeness to postulate the existence of a fourth basic two-terminal circuit element which is characterized by a ϕ-q curve. This element will henceforth be called the memristor because, as will be shown later, it behaves somewhat like a nonlinear resistor with memory.” (Chua, p. 3)
http://www.lane.ufpa.br/rodrigo/chua/Memristor_chua_article.pdf
Chua, L. O. IEEE Trans. Circuit Theory 18, 507-519 (1971).
![[Graphics:HTMLFiles/Power of Four_30.gif]](../../Memristics/Power of Four/HTMLFiles/Power of Four_30.gif)
Gunther and Chua
Thus, Gunther’s approach is augmenting reality from the M-S-T-structure by the operationality of the process P, but is not yet considering the interaction between space and time in terms of bifunctorial inter- and exchangeability.
The similar historical situation we discover with Leon Chua. “From the logical as well as axiomatic points of view, it is necessary for the sake of completeness to postulate the existence of a fourth basic two-terminal circuit element which is characterized by a ϕ-q curve.”
Also the existence of the fourth element, the memristors, was constructed mathematically and postulated physically, a new comprehensive formalism for the time- and history-dependent behavior of memristive systems is still lacking.

![[Graphics:HTMLFiles/Power of Four_32.gif]](../../Memristics/Power of Four/HTMLFiles/Power of Four_32.gif)
Complexity theory or chaos theory is describing the behavior of memristive systems externally, i.e. from the viewpoint of an external observer. Therefore, no systemic or logical self-referentiality is yet involved. But complex systems in the sense of Rosen are are involved in the mapping of the system-model relation in the very definition of the system, and are therefore implementing basic self-referentiality unknown to classical complexity theory.
http://memristors.memristics.com/Memory/Memory%20is%20more%20than%20Storage.pdf
Memristor = Fourth Element
"For now, it may help you to know that there are two technical reasons why the memristor is the fourth element.
First, one can prove from circuit-theoretic principles that it is impossible to build a memristor using only two-terminal resistors, inductors, and capacitors, even if one uses such active 2-terminal elements as negative resistors, or tunnel diodes. Following the logical principles from Aristotle, it would be only logical to classify the memristor as a different element from the other three.
Infinite number of circuit elements
"The second reason is even though Part 1 [of the 2002 paper] shows there is an infinite number of circuit elements, and even though all can in principle be built using transistors (this does not contradict my statement above since transistors are 3-terminal devices, while the memristor being a 2-terminal device, should also be realized with 2-terminal devices), only memristors can be built without transistors, op amps, batteries, etc.
All the higher-order elements are active, and hence do not exist in nature. They must be made with active elements and need a power supply.
In contrast, the hp memristor is passive and hence non-volatile. This is analogous to chemistry where elements with higher numbers are unstable, and radioactive. Hope above helps."
Thank you Dr. Chua.
http://www.frog he art.ca/?p=923
Circuit elements with memory: memristors, memcapacitors and meminductors
"This relation can be generalized to include any class of two-terminal devices (which are called memristive systems) whose resistance depends on the internal state of the system.”
"We extend the notion of memristive systems to capacitive and inductive elements, namely capacitors and inductors whose properties depend on the state and history of the system. All these elements show pinched hysteretic loops in the two constitutive variables that define them:
current-voltage for the memristor,
charge-voltage for the memcapacitor, and
current-flux for the meminductor.
We argue that these devices are common at the nanoscale where the dynamical properties of electrons and ions are likely to depend on the history of the system, at least within certain time scales.
These elements and their combination in circuits open up new functionalities in electronics and they are likely to find applications in neuromorphic devices to simulate learning, adaptive and spontaneous behavior.
Many systems belong to this class, including the thermistor (whose internal state depends on the temperature). In particular, memristive behavior is a property of thermistors, molecular systems, spintronic devices and thin film nanostructures.”
"In fact, it should not come as a surprise that many of the above examples refer to nanoscale systems, whose resistance is likely to depend on their state and dynamical history, at least within (possibly very short) times scales dictated by the fundamental state variables that control their operation.”
http://arxiv.org/pdf/0901.3682v1
http://nanomorphware.blogspot.com/2009/02/missing-memcapacitor-found.html
![[Graphics:HTMLFiles/Power of Four_34.gif]](../../Memristics/Power of Four/HTMLFiles/Power of Four_34.gif)
![FrameBox[RowBox[{ , RowBox[{Chuatronic triadic system, <br />, & ... , {0., -16.75}}, ImageRegion -> {{0., 1.}, {0., 1.}}]}]}], BoxMargins -> {{0.2, 0.2}, {0.4, 0.4}}]](../../Memristics/Power of Four/HTMLFiles/Power of Four_35.gif)
Chua’s generalizations are exploring the new field of memristics opened up by the fourth element.
The fourth is the closure of a paradigm and simultaneusly the opening of a new paradigm of electronics.
With Gunther’s fourth element of cosmology, a 3-valued logic was constructed. But this closure within 3 was at the same time opening up with his place-valued logical systems new dimensions of thinking beyond the fourth cosmological categories.
Ten years later this multiple-valued logical speculation of closing while opening up strategies got a more radical formalization with the introduction of a pre-logical sphere of morphogrammatics and the radical interaction of the closed quindecimal system of an open distribution and mediation of the 15 basic morphograms of complexity four.
With the publication of “Cybernetic ontology and transjunctional operations”, 1962, as a Technical Report No. 4, the very idea of a dialectical interplay of openness and closure moved from John Campell’s science fiction magazine “Startling Stories” to the eminent scientific location of the Electrical Engineering Research Laboratory of the University of Illinois, Urbana, directed by Heinz von Foerster and promoted by Warren McCulloch, with the National Science Foundation, Grant 17414, Washington 25, D.C. as the sponsor of the project.
As much as Chua’s fourth element is not directly visible and detectable, i.e. measurable from a micro-electronic position because it belongs to the nano-sphere, Gunther’s fourth cosmological category is unthinkable in the classical framework of logic and ontology because it belongs to a trans-subjective sphere of polycontexturality, i.e. meontics (greek me on: non-being, nothingness). The new logics invented as place-valued logics for covering the realm of nothingness and later, got a crucial radicalization by the invention of kenogrammatics (greek kenos, empty) which is covering the realm of emptiness as a radicalization of nothingness. The unthinkable might not have a mental representation in a single human observer but it might nevertheless be accessible by new ways of calculating morphogrammatic interactions.
The academic criticism of the four echoed the same pattern of defence for both speculations and discoveries: Why 4 and not 7 if there are “zillions"?
I follow the nice story told by Ketaki Kerur of Chua’s fascination for Aristotle’s theory of matter as it might be found in the compilations of the story of the beginnings of the memrsitor.
"Leon Chua compared this way of defining circuit elements to Aristotle‘s theory of matter.
According to this theory, all matter consisted of the following four elements:
Chua: ”striking resemblance"
![[Graphics:HTMLFiles/Power of Four_37.gif]](../../Memristics/Power of Four/HTMLFiles/Power of Four_37.gif)
A lively presentation of the metaphysical background and motivation of Chua’s strategy of discovery is to enjoy at the UCBerkeleyEvents “Memristor and Memristive Systems Symposium (Part 1), 2008” (0:18:49 video).
http://www.youtube.com/watch?v=QFdDPzcZwbs
Leon Chua saw a striking resemblance between the relation among elements and the relation among various circuit variables. He reasoned that there should be a fourth fundamental circuit element to complete the symmetry. He called this element, which sets up a relation between flux and charge, the memristor, short for memory resistor.
Ketaki Kerur, A study of the memristor, the fourth circuit element, 2010
http://krex.k-state.edu/dspace/bitstream/2097/4605/3/KetakiKerur2010.pdf
![[Graphics:HTMLFiles/Power of Four_38.gif]](../../Memristics/Power of Four/HTMLFiles/Power of Four_38.gif)

With the concept of anticipative systems Robert Rosen initiated another post-academic turn of an understanding of Aristotle’s Final Cause (telos) for a theory of living systems.
Robert Rosen’s Anticipatory Systems, 1985, gives the necessary orientation to the new under- standing.
"The reader will also find a number of unsuspected relationships between the notion of complexity and the old Aristotelian categories of causation. In particular, we will argue that the category of Final Cause, excluded from science for so long because of its incompatibility with the science of simple systems or mechanisms, is not excluded from the science of complex systems. A corollary is: an anticipatory system must be complex.” (ibd., p. 406)
"But Aristotle argued that there were four distinct categories of causation; four ways of answering the question why. These categories he called
material cause,
formal cause
efficient cause and
final cause.
Theses categories of causation are not interchangeable.
If this is so (and I will argue below that indeed it is) then there are correspondingly different kinds of information, associated with different causal categories.” (ibid, p. 409)

Aristotle, Rashevsky, Rosen - A common thread
http://www.panmere.com/?p=28
Daniel M. DUBOIS, Introduction to Computing Anticipatory Systems
Things are not easy to grasp, thus I give some more scholarship by citations.
"The verb anticipate comes from Latin word anticipare which means ‘to take before’. ‘To anticipate’ means to realise beforehand, to foresee, to look forward to, to act in advance to prevent, to forestall.
Robert Rosen (1985, p. 341), in the famous book Anticipatory Systems ìtentatively defined the concept of an anticipatory system: a system containing a predictive model of itself and/or of its environment, which allows it to state at an instant in accord with the model's predictions pertaining to a later instant.
Robert Rosen considers that anticipatory systems are related to the final causation of Aristotle. A future cause could produce an effect at the present time. Then the causality principle seems reversed. Robert Rosen relates some anticipatory systems to feedforward loops.
Anticipatory systems deal with the question “WHY?” related to a finality: “Why did you take your umbrella, the weather is so sunny?", "Because I thought that the weather will be bad”. Anticipatory computation deals with potential final conditions. This is the basis of the intelligence and comprehension: “to comprehend” which means also “to include as a whole".
Classical systems deal essentially with the question HOW. Recursive computation is related to a current computation as a function of past computations. The explanation is to be found in the past memory of the system and for Newtonian Systems, in the actual initial conditions.”
http://www.lampsacus.com/documents/introductionanticipatory.pdf
"We have argued that the social system can be considered as an anticipatory system in the strong sense of constructing its own future. It does so by reconstructing its past in the present. Because this reconstruction is functional to the progressive development of this system, the system can be expected to differentiate increasingly and a manifold of meanings can be entertained. The ones which are again selected, are circulated as information in a system that thus remains under continuous reconstruction.
http://arxiv.org/pdf/0912.1226v1
"Theses categories of causation are not interchangeable.” This statement is of the same kind as Chua’s proof of the non-definability of memristivity by the means of the 3 classical electronic devices and of Gunther’s insistence of the non-reducibility of the category of process P.
It might be a too strange paradox to identify a similar kind of paradigm change in Rosen’s anticipatory systems and Chua’s time- and history-dependent memristive systems. At a first glace they seem to state opposite positions in relation to the temporality of systems, complex and memristive.
With the memory of the latest state of the event in the system, the system is anticipating its future possibilities for actions.
Hence, the retrogradeness of memristive recursivity is prospecting its future possibilities.
For memristive systems, both, progression and retrogression, are second-order order concepts.
Retro- and pro-gression are the two modi of the temporality of memristive systems.
Until now, the pro-gradeness was not specifically analyzed in my papers about the temporality of memristive systems. It has to be seen that the progradeness of successions is a second-order notion too. Hence, its horizon of progression is enabled by the future-aspect of the retro-gradeness.
Classical formal systems are depending on their alphabet only to produce step-wise continuations. The rules of the system are not in anyway restricted by the past state or constellation of the system. Hence, prolongations are not framed by a concrete “time- and history-dependent” horizon of production.
Memristive systems are retro-/prograde anticipatory systems.
The state of a memristive system is stored, i.e.memorized by the system in absence of a current. If a new current is active it will encounter the resistance of the last activity. This is an condition from the past. But it is, at the same time, a condition for the new event posed by the future of the event.
Hence, time-dependence has two faces: one for the system (and its past) and one for the new event of the system.
The new event is confronted with what happened before as the anticipated horizon of its new realization.
The future horizon of a new event is defined by the memorized state of the past of the system.
What seems to be obscure and nonsensical is depending on the presumption of the classical world view which is excluding in advance the category of a final cause.
On the other hand, because of the non-interchangeability of the 4 causes, i.e. non-definability of the final cause by the other three causes, it is impossible to reach an agreement in the debate.
It seems that with the advent of memristive systems some new experiences and arguments in favor for the fourth principle are becoming accessible.
"But there is no final cause in this picture. Indeed, as Ashby noted, the moment of final cause would have to involve a notion of the future acting on the present; of future state or input affecting present change of state; of anticipation. This is resolutely excluded, once we have decided that the category of dynamical (i.e. “state-determined") constitutes the only acceptable class of mathematical images of the external world.” (R.Rosen, The physics of complexity, in: Power, Autonomy, Utopia, (Ed.) Robert Trappl, Vienna 1986, p. 39)
On the conceptual level of first-order objects it is for sure utterly absurd to think or belief in a power like a temporal future to have an influence and determination on actual and past events. Just for that reason everything around a causa finalis, teleology, vital force and vitalism as such had been refuted by modern science.
Again, the presumption in the play is time, the existence of time as real or transcendental, and the linearity of time organizing an ordered chain of past-present-future events.
This kind of absurdity of category mistakes becomes even more obvious if we connect the memristivity of memristors of a memristive device with the time- and history-dependence of memristive systems involving anticipatory features to realize their located behaviors of retrograde recursivity and chiastic interplay of memory and computation.
If there are four causes then there must also be some kind of an order or organization of the causes. It remains as an open question to which cause the principle of the organization of the causes belongs.
In the framework of traditional metaphysics, ontology and epistemology the order of causes is conceived, for logical reasons, as a linear succession. At least no two causes are responsible at once for the state of an event.
"The essential point is that, in the Newtonian picture, these categories are isolated into independent mathematical elements of the total dynamics.” (ibd., 19)
In contrast to the discussed approaches of Gunther, Chua and Rosen, this paper is promoting the idea that the independence and simultaneity of causes or categories or elementary elements is a precondition for the new and yet unthought possibility of a metamorphosis of those autonomous interrelated and interacting categories. Without such an independence a radical change, and at once a stable preservation of a category, such a transformation of a category into another category wouldn’t be possible. Such metamorphosis as an interplay of change and preservation is not to confuse with the ideas of emergence studied by complex systems theory.
A transition of the roles of causes from the Aristotelian independence of causes to an interaction and metamorphosis of causes seems to be the challenge of a science based on the design of complex systems.
"Now let us return to the main line of the argument, and look briefly at what happens when we abandon the requirement that the categories of causation must be represented in independent mathematical structures. This means, in Ashby’s terminology, that we give up the idea that each “variable” of a system can be classified as belonging exclusively to the category of material cause, or exclusively to the category of formal cause, or explicitly to the category of efficient cause.
In other words, we allow that some, and perhaps all, variables simultaneously participate in two or more of these causal categories. Then what happens?” (ibd., p. 40)
"What happens, of course, is that we must allow a wider class of mathematical images of physical reality than dynamical systems, or"state-determined” systems, to which system theory has hitherto restricted itself.
These mathematical images becomes more like webs of informational interactions, no level of which can be derived from any others.” (Rosen, ibd., p. 40/41)
Slogans
Prediction is not anticipation.
Anticipation is the precondition of realization.
The preconditions of a realization are the saltatories of the realization.
A realization is a system defined by categories where the categories are defined by the saltatories.
If memristive systems have properties of anticipatory systems in the sense just sketched, the inverse question, Do anticipatory systems have memristive properties? is not yet been in the focus of thematization. What is the retrograde recursivity of anticipatory systems as they have been introduced by Robert Rosen as complex systems in contrast to the classical simple systems?
It seems that anticipatory systems which are based on model-theoretic decisions are not reaching the concreteness of locatedness of memristive operations and systems. They remain in a domain of conceptuality which is defined by the modeling approach.
Memristive on the other side are modeling and constructing their retrogradness from a bottom-up position while anticipatory systems are involved by modeling in a top-down approach.
Recursion, incursion and hyperincursion
"In addition such relationships have proved to be an essential feature in anticipatory systems - the construction of systems which are tentatively defined as those for which the present behaviour is based on past and/or present events but also on future events built from these past, present and future events.
"An incursive system is more than just a recursive one. An incursive discrete system is a system which computes its current state at a particular time, as a function of its states at past times, present time and even its states at future time.
"A hyperincursive discrete anticipatory system is an incursive discrete anticipatory system generating multiple iterates at each time step. Incursion corresponds to weak anticipation and hyperincursion to strong anticipation.

”Now, all anticipatory systems are living systems, is this true?” in an interview [Rosen] replied cautiously ”Well, all that we know about”.
Dubois considered that anticipation is not only a property of biosystems but is also a fundamental property of physical systems.”
M. A. Heather, B. N. Rossiter, Information Systems and the Theory of Categories: Is Every Model an Anticipatory System?
http://computing.unn.ac.uk/staff/cgnr1/liege04m4.pdf
"Anticipation is therefore more fundamental than either time or space.”
"Anticipation is the natural preordering on any system.”
http://computing.unn.ac.uk/staff/cgnr1/liege09space%20abs.pdf
There might by a hidden chain of conceptual connections and transformations to be discovered in the work from Asimov’s Jump, Gunther’s Process, Rosen’s Anticipation and Chua’s Harmony to the idea of a diamond-theoretical interplay between categories and saltatories, also called “Jumpoids".
Hence there might be a common transformation formula discovered behind those paradigmatic changes.
Firstly, the transition from a simple, classical and an electronic systems to a complex, trans-classical and a nano-electronic paradigm is involved in the transformation from a triadic, trinitarian and 3-fold conceptuality to a ternary and 4-fold framework of conceptualization.
Similar holds for the transition from a category-theoretic to a diamond-theoretic conceptualization. This transition is connected to the non-concept of a “Jump”. There is no natural logical or causal extension from the classical to a trans-classical epistemology. All extensions, conservative or not, are remaining in the framework of the classic approach. There is a kind of an epistemological closure and uniqueness of the classical conceptualization.
What is missing in the described approaches of a transition from a ternary to a quaternary epistemological thematization is an implementation of this “jump” inside the formalisms of the new model.
Up to now there are no jump-operations implemented neither in Gunther’s polycontextural logics, nor in Chua’s memristive system theory or in Rosen’s modeling of anticipatory systems. All operations are still in one or the other way ‘homogenically’ composed in the sense of composition in category theory. There are also no ‘jumps’ between different categories of different categoriality.
From a diamond strategic approach, the rupture between the old and the new has to be ‘mirrored’ inside the new.
One solution for this approach is given by the saltisitions, i.e. jump-operations, of saltatories of diamond theory. To become accessible, it is necessary that the new formalisms have some degree of complexity and complication.
Traditional category theory as it was originally conceived in the Scottish Café in Lwow (Poland) in the 1930s and 1940s, is in its definition triadic even if its intention later by Saunders Mac Lane was the quaternity of natural transformation. Hence a diamondization of a triadic concepts offers just a singular hetero-morphism of a saltatory but not yet the gap between heteromorphisms. This is established for a fourfold structure with two hetero-morphisms demanding a jump to be connected. The jump or saltition is a new property which is not realized by any iterative application of the triadic concept.
![]()

It could be said that the gaps between hetero-morphisms in saltatories occur automatically with an iterative extension of single triadic diamonds to ternary compound diamonds. But the jump operation, between different hetero-morphisms is not automatically given by such a conservative extension.
As much as “every statement, theorem, or definition in category theory has a dual” each duality in category theory has a complementarity in the theory of saltatories of diamond theory.
Categories
Structure: composition and identities, for the
Properties: unit and commutativity axioms. All based on
Data: arrows, with source and target. Fulfilling the matching conditions for arrows.
Saltatories
Data: counter-arrows
Properties: diversity and jump-law
Structure: saltisition and differences.
Diamonds
complementarity
interplay
bi-objects.
Arthur Schopenhauer, Über die vierfache Wurzel des Satzes vom zureichenden Grunde, 1813/1847
All examples of transcending classical cosmology, systems theory, ontology and electronics might be covered by the concept of a simple diamond. A simple diamond is a diamond with a restricted complexity to the level 3 + 1, i.e. the triadicity of the structure plus the unicity of its “otherness” as process, environment or nanosphere.
It seems that Chua’s approach to generalized memristive systems has the power to surpass such singularity of the 3+1 concept and is opening up with the concepts of memristance, memcapacitance and meminductance, i.e. with mem-x, realms of complex nanoelectronics.
Gunther’s approach surpassed this limit later with his theory of polycontexturality including transjunctional operations and kenogrammatic transitions as combinations of iterative and accretive kenogrammatic operations.
I’m not yet aware in which sense Rosen’s approach of complex systems is transcending the 3+1 concept.
From a grammatological point of view it is interesting to see that all 3 approaches are involved in mixed textualities of philosophical or epistemological notions developed in texts and mathematical and electronic and experimental formulas and actions.
This is in strong contrast to the ‘new movement’ of “speculative realism” or “object-oriented philosophy" (Brassier, Ray, Iain Hamilton Grant, Graham Harman, Quentin Meillassoux) which is deadlocked in its own narration, lacking any complementary textu(r)ality, operativity and technical visions.
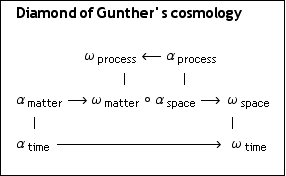
Cosmology:
(M , T , S), P => (M o T o S)| P
M : matter,
S: space,
T: time,
P: process.
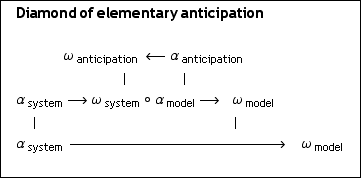
Anticipation:
( system, model ) => ( system, model )|non-model
simple system: ( system o model )
complex system: ( system o model )|![]() .
.
A diamondization of the classical system-model relation is uncovering its complementary “non-system/model relation” as its saltatory system.
cod(system) ≅ dom(model), i.e. ωsystem ≅ αmodel
For the classical paradigm of science which is studying according to Rosen, simple systems, anticipatory systems which are conceived as complex systems are understood as playing the role of the environment of simple systems.
A complex system is negatively defined by Rosen:
“A system is simple if all its models are simulable. A system that is not simple, and that accordingly must have a nonsimulable model, is complex.”
http://www.panmere.com/index.php?page_id=16#en20
Within the diamond approach we can positively or constructively define a complex system as an interplay between categorical simple systems and its saltatorical environments, i.e. saltisitions.
On the other hand, a simple system is a complementary system of a complex system on a categorical level. Hence, the definition of simple and complex systems is given as a complementarity in a diamond theoretical formalism.
A more complex modeling of the anticipation scheme is achieved with the implementation of saltisitions between (hetero)morphisms. Hence, between the environmental system and the environmental model, ![]() , relative to the simple system and model, ( system o model ), is ruled not by representational composition, model-mapping or any other category-theoretic constructions, but by “jumps” (saltisitions).
, relative to the simple system and model, ( system o model ), is ruled not by representational composition, model-mapping or any other category-theoretic constructions, but by “jumps” (saltisitions).
diamond complex system: ( system o model )|![]()
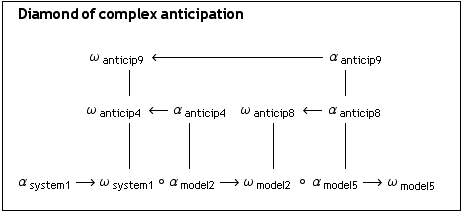
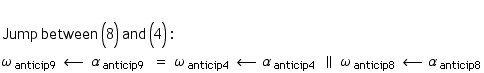
Complementarity to the jump: A risky bridge
The semiotician Alfred Toth applied another diamond theoretic construct for his new kind of semiotics: The risky bridge. Concerning the interplay of categories and saltatories, the gap between hetero-morphisms might be ‘bridged’ not only by a jump-operator or a “spagat” but also by a bridge. This bridge is introducing the action of bridging between categories and saltatories as an action complementary to the jump. Because this action involves both parts of a diamond, the categories and the saltatories, it was called a “risky bridge”.
Following the diagram, the “risky bridge” is build by the hetero-morphism salt8, salt4 and the morphism morph2. Hence salt9 = salt4 ; cat2; salt8.
"However, if we now take as a model for sign-composition out of sub-signs the following polycontextural 4-adic diamond, taken also form Kaehr (2007) then we have got a third type of semiotic mapping: “We can bridge the separated arrows by the arrow (kl), which is a balancing act over the gap, called spagat. If we want to compromise, we can build a risky bridge (lgk), which is involving acceptional and the rejectional arrows” (Kaehr 2007, p. 12).
Kaehr, Rudolf, The Book of Diamonds. Glasgow 2007. Digitalisat:
http://rudys-diamond-strategies.blogspot.com/2007/06/book-of-diamonds-
intro.html (2007)
Alfred Toth, Semiotic “risky bridges” vs. “spagat” in 4-contextural tetradic semiotics (NETS, 12) http://www.docin.com/p-104914781.html
Fourfoldness of diamonds
Hence we are back to a reasonable and operative fourfoldness of categories, saltatories, jumps (saltisitions) and bridges of diamond theory.
Chua’s memristive diamond
In this example of a model, capacitance is internally dual to inductance, and resistance therefore is complementary to memristance. The pair (resistance, memristance) is not dual like the pair (capacitance, inductance) because memristance is not set inside the system of electronics of (capacitance, resistance, inductance) but “beyond” such a system, i.e. opening up the ‘metasystem’ of the system in the sense of Palmer’s Emergent systems theory. This becomes quickly clear if the modes of composition (categorical versus saltatorical) are studied in more complex situations.
Categorical composition is gap-free, saltatorical combinations are involved in ‘jumps’ over gaps. As the example makes it clear enough, diamondization is not introducing a metasystem in the sense of classical model theory of logic, cybernetic systems, etc.
http://www.scribd.com/doc/30166581/Memristics-Memristors-again
![[Graphics:HTMLFiles/Power of Four_51.gif]](../../Memristics/Power of Four/HTMLFiles/Power of Four_51.gif)
![[Graphics:HTMLFiles/Power of Four_52.gif]](../../Memristics/Power of Four/HTMLFiles/Power of Four_52.gif)
From gap-free compositions to saltatorial jumps
This presentation is using a kind of a "tour de force” strategy because the hidden matching conditions are not (yet) explicitly introduced. What nevertheless becomes more clear is the difference of sequential (or parallel)gap-free compositions (yuxtapositions) for electronic systems and the saltatorical (salto: jump) combinations in memristive systems. With an elaboration of this diamond-theoretical construction, a clear conceptual and paradigmatic difference (rupture) between electronic and memristive systems would be established | probably as a sine qua non of memristics.
The first kind of jumps, obviously, is opening up the nano-electronic sphere. The second ‘compositional’ jump might be identified as the jump between different memristive layers in a multi- or poly-layered crossbar system.
Memristance as an environment of electronics
It could be argued that the electronics of (R, C, I), i.e. resistance, capacitance and inductance, is building a categorically closed, i.e. simple system. Therefore, memristance occurs, conceptually, as an environment of this closed system. Therefore, memrsitive systems which are including classical electronics with memristivity as its environment are complex systems in the sense of Rosen.
With such an interpretation of memristive systems as complex systems questions of mathematization and decidability occur in a new light.
"Rosennean simplicity is a relational property of a system if all the models of the system are Turing-computable.
Rosennean complexity is a relational property of a system if at least one of the models of the system is Turing-incomputable."
http://www.panmere.com/index.php?page_id=16#en20