Sketch on semiotics in diamonds

Embedding semiotics into anchored diamonds

Rudolf Kaehr Dr.^@

ThinkArt Lab Glasgow

Abstract

Semiotics are embedded into diamonds in a double way. Semiotics gets a internal environment as its neighbor semiotics and an external environment by its anchors. Embedding semiotics is a process of concretization of the abstract concept of Peircean semiotics.

1.  Diamond embedments of semiotics

1.1.  Semiotics within semiotics

Introduction of the semiotic scheme by Bense/Toth:

An extensive study of a relational introduction of the Peircean semiotics is presented in [Toth, Einführung in die semiotische Relationentheorie]. Additionally, a further development to a ternary semiotics and its relation to Gunther’s ternary epistemology is proposed.

1.1.1.  Diamondization of semiotics

A diamondization of the semiotic scheme is naturally realized as a diamond interpretation of the semiotic relations, i.e. morphisms.

Firstness as a doublet
A composition always is accompanied by an environment of its morphisms. Therefore, an initial object or the number 1, firstness, is diamond theoretically always doubled: as itself and as its environment, i.e.( A | a). That is, as a morphism, and as a hetero-morphism. A diamond initial object is not a singular object but a doublet. Also called bi-object. Furthermore, self-identity is able to distinguish its directionality as left (lo) and right (ro) order.
    

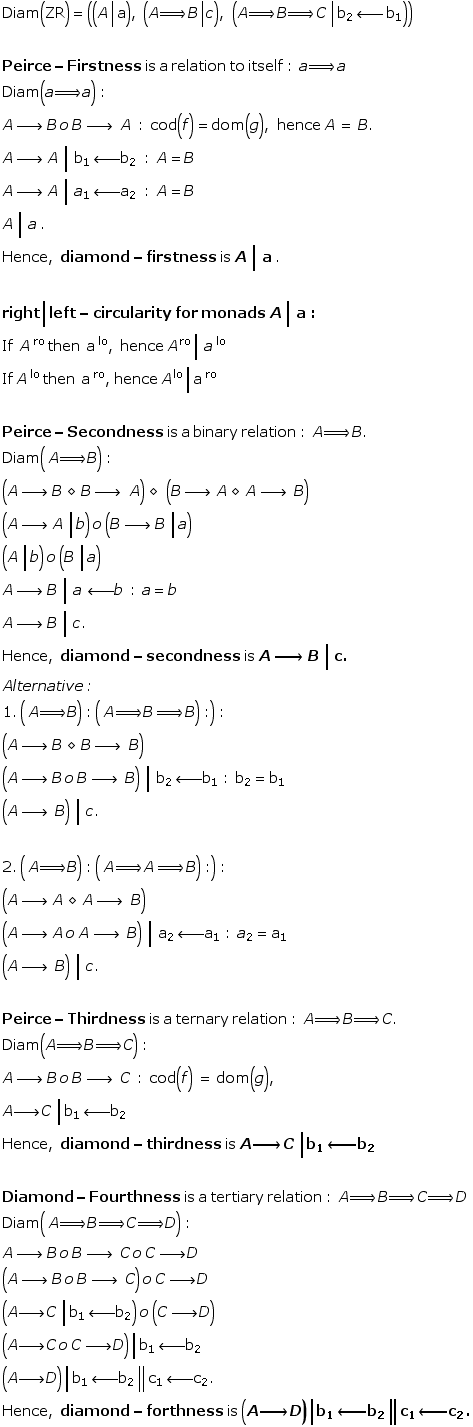
Comments¹
Therefore,
Firstness is a relation to itself, a ‘monadic’ relation:
a as a a is a reduction of aaa.
Secondness is a binary or ‘dyadic’ relation:
ab is a reduction of abb, aab.
Thirdness is a ternary or ‘triadic’ relation:
abc is a realization of the intuition.

Classificatory remarks²

In Transit (Toth, 2008)³

For a start, it might be a significant result to proof the difference with the simple example of Toth’ s dually invariant sign class , which is, as it turns out, contexturally different, i.e.

This, obviously is based on a different paradigm and its duality results for identity:

1.2.  Diamond semiotic values

1.2.1.  Semiotic values

Semiotic principle for sign classes according to Bense/Toth

1. Principle of Triadic Diversity:
The general sign class structure has the form (a.b c.d
e.f) with a, b, c, d, e, f ∈ {1, 2, 3} and a != b != c.

2. Principle of Degenerative Triadic Order:
The general sign class structure must have the form (3.a 2.b 1.c).

3. Principle of Trichotomic Inclusion:
(3.a 2.b 1.c) with a <= b <= c and a, b, c ∈ {.1, .2,.3}.

"However, we may question if the three semiotic restrictions do hold. From the standpoint of relational algebra, nothing speaks in favor of the Principle of Semiotic Inclusion.”  (Toth, Ghost, p. 10)

1.2.2.  Mediation of semiotics

1.2.3.  Ternary semiotics as composed by binary relations

If unary triadic signs are defined as compositions of dyadic sub-signs then their compositions to binary and ternary triadic sign systems should have a natural decomposition into their sub-signs.
A natural decomposition is guided mainly by its mathematical constructions and not by any content or other interest oriented restrictions to formal procedures.
If a composition is a sign then all its permutation have to be accepted as signs.

1.2.4.  Semiotic vs. polysemiotic sign classes

1.2.5.  A special case, ?

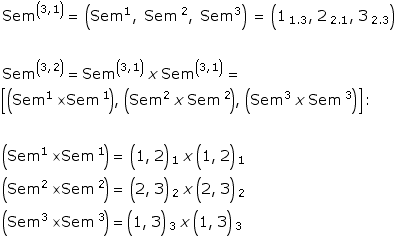
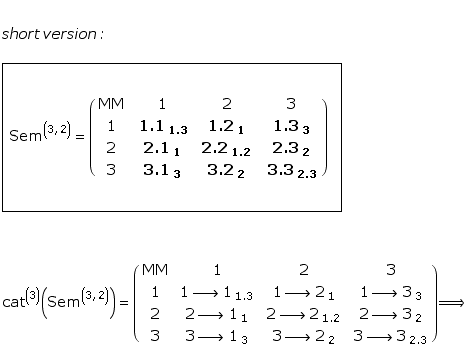
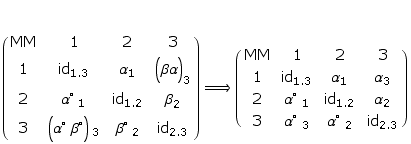
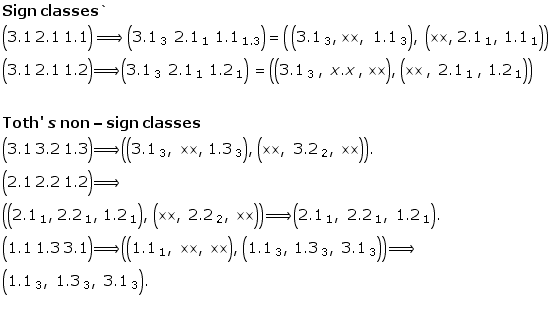
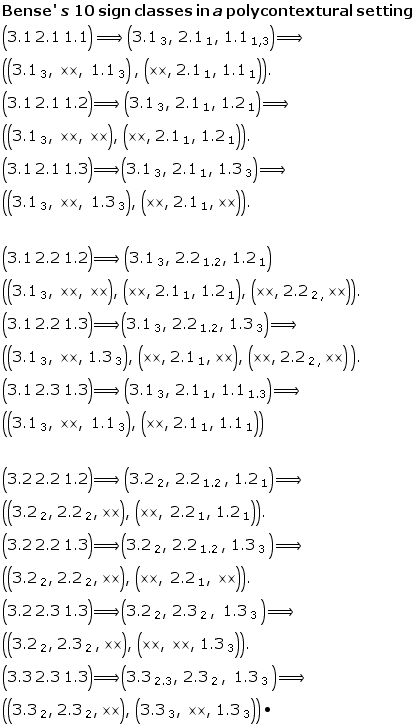
Toth mentions a special case in his new classification of sign classes:  (3.1 2.2 1.3 ) x (3.1 2.2 1.3), which is "the dual invariant sign class”. (Toth, Ghost, p. 14)

A polycontextural micro-analysis of the duality shows a subtile difference which is not confirming in detail the “dual invariance” of Toth’ s mathematicl semiotic approach to sign classes.

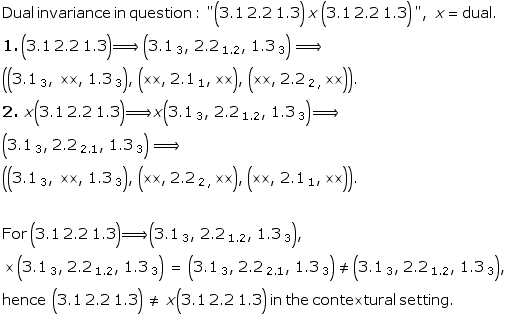
The special case of a dual invariance, (3.1 2.1 1.3) x(3.1 2.2 1.3), doesn’t hold in a polycontextural setting because the decomposition shows the inverse order of (2.2_1.2) in the dual case, i.e.
(2.2_1.2) != (2.2_2.1).

Non-Peirce-Bensean self-dual sign classes⁴

Duality, identity and reflectionality.⁵

1.2.6.  Diamond semiotics abstract scheme

This kind of presentation (cf. Toth, Ghost, p. 13) is intended to give an idea of the embedment of semiotics and its diamond environments as a further ‘external’ embedment of semiotics. Hence, semiotics in polycontextural diamond constellations are towfold embedded 1. by their neighbor-semiotics and 2. by their diamond environments. Obviously, semiotics and diamond environments are equiprimordial (gleichursprünglich). In a further step of concretization, the construction gets its localization as a 3. embedmend by its place-designators of the kenomic anchors. ⁶

1.3.  Diamond semiotic interpretations of (M, O,I)

1.3.1.  Semiotic interpretation

Independent of the reasonability of the decision to introduce meaningful interpretations to the numeric classification of sign and sub-signs into object, O, medium, M, and interpretation, I, with its differentiations into sub-distinctions, the distinctions are made in the mode of is-abstractions. That is, the decision to interpret, e.g. 2.1 as M(I) = sin-sign, is definitive and identical in all possible semiotic contexts. No sin-sign can change in its use to a legi-sign or to a symbol. This fact is further proof of its identity heritage from classical ontology and logic.
Possibilities of thematizations are augmented in the case of embeded semiotics.

1.3.2.  Polysemiotic interpretations

1.3.3.  Diamond semiotic interpretations

2.  Anchored diamonds

2.1.  Anchored semiotics

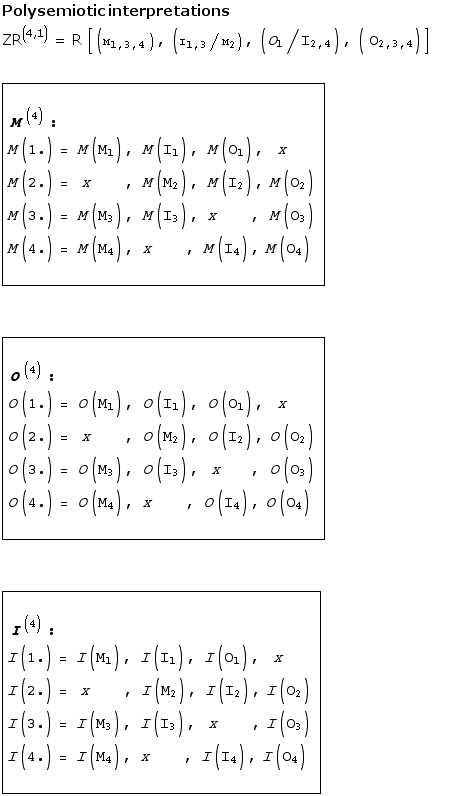
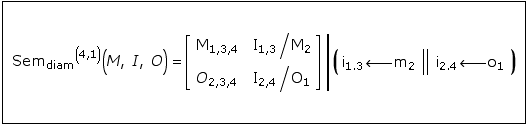
Semiotics are conceived by Bense/Toth as anchor-free.⁷

2.2.  Anchored diamonds

2.3.  Dissemination of diamonds

2.3.1.  Disseminated semiotics

2.3.2.  Disseminated diamonds

Notes

2

Classificatory remarks As a first result, I would like to point to the scenario, which could be misunderstood. To construct an embedment of semiotics into diamonds doesn’t establish a priority of semiotics over diamonds. Diamond of diamond theory, like diamond semiotics, are not results of trichotomic semiotics, neither of their application. As much as diamond category theory is not part of classical category theory (in all its forms), diamond semiotics is not part of semiotics (and all its forms, say, with retro-semiosis). The same pattern holds for the topics like “Lambda Calculi in polycontextural situations”. The reason is simple. Neither for category theory nor for (mathematical) semiotics (Toth), an interplay between categories and saltatories, categorical composition and saltatorical saltisition (jump-operation), exists. Hence, a reconstruction of diamonds in the framework of semiotics or category theory is, albeit its reductive results, missing the point. Hence, semiotics (and categories) are defined by objects, morphisms and composition of morphism, and are not including the concepts of separation, hetero-morphism, saltisition and bi-objects and their specific rules. Neither co-algebras, co-categories or n-categories nor retro-semiosis and similar can be considered as proper concepts and methods for concretizations and realizations in diamond studies. Again, nevertheless, it might produce interesting results in applying such concepts for reasons of modeling and simulation in contrast to realization. On the other hand, there is no reason too, to restrict sign theory to the paradigm of Peircean semiotics (as it is represented by the Stuttgarter School). The same holds for category theory. Hence, the term semiotics might be properly used in constellation with diamond theory, polycontexturality and kenogrammatics.

3

In Transit (Toth, 2008) Interestingly, there is a highly sophisticated study accessible by Toth which is on the way to abolish, step by step, the arbitrary (and ideological) restrictions to semiotics as they had been superimposed by Bense for interpretational reasons and in disharmony with the formal possibility of semiotics as such. Personally, I just got access to In Transit and other free downloadable e-books from UNI Klagenfurt| Reihe KBT: Toth, Alfred, In Transit. A mathematical-semiotic theory of Decrease of Mind based on polycontextural Diamond Theory. Klagenfurt 2008 It is therefore not yet the place to go into more details to compare mathematical and polycontextural diamond semiotics more properly.        Albeit the fact that Gotthard Gunther fully accepted my approach of a dissemination of formal systems as an approach to formalize his polycontextural logic, similar philosophical and anti-formalistic restrictions had been superimposed by Gunther and his followers.

4

Non-Peirce-Bensean self-dual sign classes Additionally to the special self-dual sign class "(3.1 2.2 1.3)" of the 10 accepted sign classes, all other self-dual sign classes, not included in the  Peirce-Bensean semiotics, should be accepted. Hence the sign sets, (3.2 2.2 2.3) as a general sign class/set and (2.1 2.2 1.2) as a non-sign class, or (1.2 1.1 1.2) too, are self-dual and structurally, in general, not different from the special case "(3.1 2.2 1.3)" of the privileged 10 sign classes. In general, all self-dual sign sets (x.y idi y.x), i=1,2,3 seems to be special sign classes. A main argument against restrictions in the definition of sign classes might be the fact that accepted operations on signs are able to transform accepted sign classes into non-accepted sign class, then called sign sets. It should be mentioned at this point, that a self-dual identive sign class like (1.1 1.1 1.1) has different representations in a polycontextural setting: For (1.1 1.1 1.1) = (id) = x(id) in mathematical semiotics, in contrast, the duality x(id Some additional information about distributed identity relations. 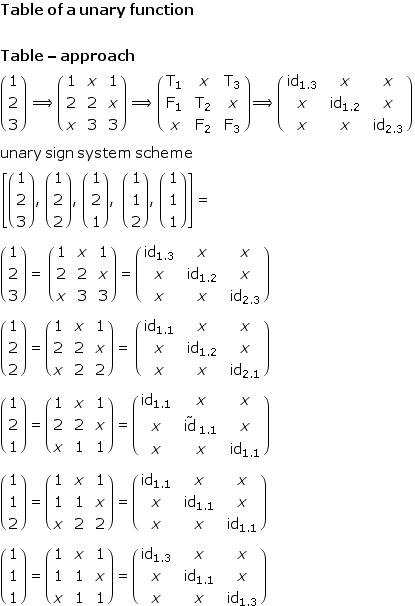        Matrix-approach 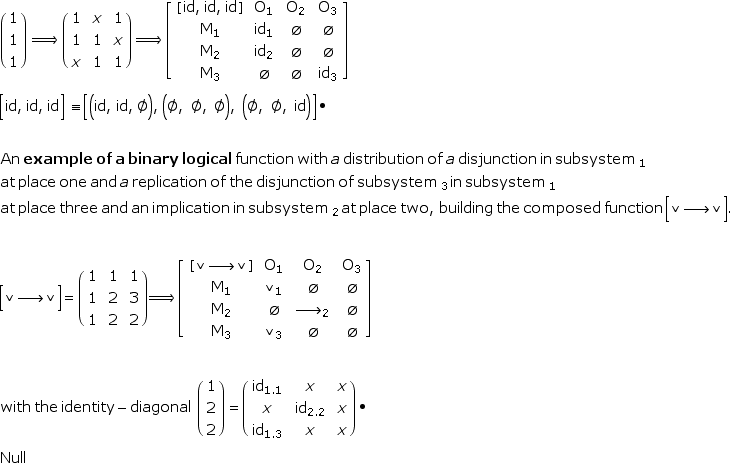        Explicit presentation at:

5

Duality, identity and reflectionality As long as identity relations in formal systems aren't involved into reflectional interactions, the whole system remains classical. Hence, semiotics of whatever formation, which aren't deconstructing their identity relation have to be classified as classical. Therefore, Toth's transclassical approaches to semiotics are doomed to fail their intentions to overcome classical restrictions. Reflectionality of identity is possible only if the thematized identity is embedded in a polycontextural environment with neighboring identity systems from whom it can be differentiated. Identity in classical systems is neighbor-less and hence not able to reflect itself.

6	http://www.thinkartlab.com/pkl/lola/Xanadu-textemes/Xanadu-textemes.pdf

7

Anchors          This free-floating illusion of anchor-free semiotics gets a concretization in the anchor-concept as it is constitutive by definition for diamonds. Anchors are realized in a kenomic grid. This happens at first as a proto-numbering of anchors. Anchors of diamonds, and as a consequence of semiotics too, are not part of diamonds or semiotics. That is, anchors are not represented by diamond’ s firstness, secondness, thirdness and fourthness. Because anchors are realized in a kenomic grid, there numeric representation level shall be 0, hence Zeroness, also understood as Emptiness or Voidness. It presents the fifth category of anchored diamonds.          Toth introduced zeroness in his new design of transclassical semiotics. A comparision of both approaches is forthcoming. Why do we need anchors?          People might be afraid to be anchored. For them it is natural to be anchor-free because their natural anchoring has become unconscious and works in the blind spot of Western rationality.          Others, who have freed themselves from anchors and have enough from the free-floating delirium of anchor-less hallucinations, understand that to be free means to be free to anchor and to dis-anchor freely in multiple ways. Hence, a freed theory of free anchors is necessary to be free.