THE LOGICAL STRUCTURE OF EVOLUTION AND EMANATION *1)
GOTTHARD GUNTHER: When I decided to accept Dr. Roland Fischer's generous invitation to read a paper at this conference I felt somewhat like a forger who passes on his counterfeit money to an unsuspecting public. It has been a time-honored tradition to say that logic and its laws are timeless and of eternal validity. This viewpoint has, of course, sometimes been subjected to a sceptical scrutiny, but all attempts to analyze time with the means of a logical calculus have come to nothing. Consequently, since the traditional viewpoint seems to be the correct one, it follows that a logician at a Time Conference should be a
persona non grata, and the currency with which he pays for admission should not be acceptable.
However, I feel that my presence has some justification. The logic discussed in all previous confrontations between Logic and Time was invariably the classic two-valued logic; but it might be proper to raise the old issue again when a logician claims that our traditional theory of thinking is not the only one and that a trans-classic system of rationality might be able to tackle the problem of time if more powerful methods of investigation were available. Since the classic theory of rationality is indissolubly linked with the concept of value, first of all one has to show that the whole "value issue" covers the body of logic like a thin coat of paint. Scrape the paint off and you will discover an unsuspected system of structural forms and relations suggesting methods of thinking which surpass immeasurably all classic theories. This was the purpose of my paper "Time, Timeless Logic and Self-Referential Systems." The trans-classic order which we discover beyond the classic theory of logic was called "kenogrammatic structure."
However, there seemed to be some doubt as to how I arrived at that kenogrammatic concept, and limited time permitted no discussion of the transition from value to kenogram. Consequently, the quintessence of my procedure seems to require some detailed explanation. Such an explanation I have given in an earlier publication,
[21] but, alas, only in strict logical terminology which may make it again difficult for an interdisciplinary audience to follow. In this dilemma, I turned to my colleague Heinz Von Foerster, a veteran in interdisciplinary meetings, to help out. He suggested that I present the development of these concepts in a mathematical vocabulary. But since this vocabulary is not my vehicle of mental propulsion, I let Von Foerster tell his story in his own words.
HEINZ VON FOERSTER: Perhaps the easiest way to see the emergence of the concept
Kenogram is to see it through the concept of the "inverse" of a logical function. The inverse of a logical function is derived in precise analogy to the inverse of a mathematical function.
Let y = f(x) be a mathematical function in which the "dependent" variable y is expressed in terms of the "independent" variable x, say y = x
2
with f(x) = x
2. Inversion is accomplished when the independent variable y is explicitly expressed in terms of the dependent x:
maintaining, however, the original functional relationship between the two variables. In the above example y = x
2 , the inverse function is
Please note two points in connection with the inversion of functions. The first point refers to the conservation of the domain of x and the range of y before and after inversion. The second point refers to the possibility of a unique function becoming a multiple-valued function after inversion or vice versa.
Let me exercise these two points on the above example. If we wish to remain in the realm of real numbers, then in the expression y = x
2 the domain of the independent variable x is the set of all real numbers and the range of y, the dependent variable, is the set of all non-negative real numbers, while in the inverted form the domain of the independent variable, now y, is the set of all non-negative real numbers and the range of the dependent variable, now x, is the set of all real numbers. This is clearly seen if one wishes to use a negative real number as an argument in the inverted function. The result is a complex number, in contradiction to our premise to stay in the realm of real numbers.
The second point of the emergence of multiple valuedness after inversion is easily seen by the (+) and (-) sign in front of the square root. For y = 4, for instance, the inverse of y = x
2 produces indeed the two solutions x
1 = + 2 and x
2 = - 2 as suggested by the expression for (+ 2 )
2 and (-2 )
2 both equal to 4.
I turn now to the inversion of logical functions where, hopefully, it can be seen that Gunther's kenograms are nothing else but the original dependent variables becoming independent after inversion. Since the range of the dependent variable in logical functions is restricted to the number of values m in the logical system, e.g., m = 2 in a two-valued logical system, and since one deals here with logical systems that admit only a few values (i.e., m is a small integer), I believe it is quite legitimate to use simple geometrical forms, say triangles, squares, etc., for representing various variables, rather than the mathematician's x, y, z, etc. However, let me continue for a moment with the mathematical notation.
Let X
n = {x
0, x
1, x
2,
�, x
n-1} be the independent variable in a logical function
where X
n is represented by an n-tuple of independent elementary variables x
i (i = 0
� (n - 1) ). The domain of these elementary variables x
i depends upon the choice of the valuedness of m of the logical system under consideration. In the classical two-valued system one has, of course, m = 2. Consequently, since the domain of x
i is m, the domain of the independent variable X
n is the set of all natural numbers between 0 and (m
n - 1), i.e., comprises m
n values.
The
modus operandi of a logical function is to associate with each of the m
n values of the independent variable precisely one value of the dependent variable y, the range of which is identical with the domain of the elementary variables x
i. A particular logical function is defined if for each of the m
n values of X
n a particular value for y within the range m is specified. This restriction produces a variety of precisely
different functions in an m-valued logical system with n independent elementary variables.
If I am not mistaken, in the history of the development of logical functions there exists nowhere a discrepancy in the terminology of "values" and "variables." These terms are used exactly in the sense as I used them before. However, a considerable variety in the use of
symbols and in the
interpretation of these symbols representing the "values" of these variables is to be noted.
Let me stay, for the moment, within the classical case of a two-valued logic, i.e., m = 2. One will find the two available values being represented in a variety of ways, for instance W, F (for "wahr", "falsch"; Wittgenstein); or T, F (for "true", "false"; Russell); or 0, 1 (Boole, Hilbert); or 1, 2 (G�nther), etc. This variety of symbolic representation of the variables leads, of course, to a variety of representations of one and the same logical function as I shall demonstrate on one particular logical function, namely, the logical "and" symbolized by "&," and also sometimes called the "logical sum" or the "logical product" (
�) of the elementary variables x
0 and x
i.
If (x
i) and (x
�) are interpreted as propositions, then it is clear that the representations (i) (ii) give the " truth- values" for the proposition "x
i & x
0", for "x
i and x
0" is only true (T, W) if and only if both x
i and x
0 are true separately. Otherwise, "x
i and x
0"
is false (F). Representation (iii) makes use of the oddity that if "true" is represented by the integer "one" and "false" by "zero" then the truth-values for the logical "and" are obtained by algebraic multiplication y = x
i � x
0. In (iv) the representations for "true" and "false" by the integers 1, 0 is reversed and the values for y are obtained by a pseudo- arithmetic addition in which 1 + 1 = 1. This latter interpretation of the integers 0, 1 has, however, the advantage that the logical function "inclusive or" can be represented as a proper algebraic product
I apologize for this somewhat lengthy narrative on an otherwise well-known story. However, I wished to stress in this account the arbitrariness by which certain symbols may be associated with two-valued logical values "true," "false" or "position", "negation," etc. In the above examples, "true" was in one case associated with integer "one" and in the other case with integer "zero," and
mutatatis mutandis:
With this introduction, I believe it is now easy to understand G�nther�s mysterious triangles in example (v). Let the upright empty triangle stand for the integer 0 and the downward full triangle stand for the integer 1, then the function represented in example (iv) is obtained. If, moreover, T
� 0 and F
� 1, example (v) represents the logical function "&", which symbol may now be inserted into the yet empty space on top of the column representing y.
However, there is no need to insist on the interpretation suggested above, and we may as well reversely identify the upright empty triangle with the integer 1 and the other one with 0. But since this reversal does not affect the values of the independent variable x
2-a particular triangle is associated uniquely with a
set of values Of X
2, namely
such a reversal will alter the logical function:
I hope that this simple example clarifies the meaning of those symbols that G�nther called "Kenograms" and which are represented here as triangles of different shapes. Since kenograms may assume different values, but different kenograms not like values:
they may be considered to be "elementary variables" y
i of the dependent variable y, with the condition
their range being the number of values m of the logical system. The indices i, j may assume values of the integers 1
� r
� m, where r is the number of different values admitted to occur in the dependent variable. For example, r = 1 suggests that the dependent variable y admits only one value. For logical functions that are confined to two variables only (n = 2), this situation (r = 1) is given by the following scheme
in which by the particular sequence of like kenograms the logical functions C and T are represented which, in turn, may stand respectively for "Contradiction" and "Tautology," but only if "0" is associated with "true" and "1" with "false."
A particular sequence of kenograms has been called by G�nther a "morphogram", M. However, such a "sequence" is not invariant to permutations of the sequential arrangement of the values of the independent variable X
n, The invariance of the association of a kenogram with a particular value of X
n, and hence the invariance of a morphogram with respect to permutations in a particular sequential arrangement of X
n can be established by defining the set of values X
ni which are associated with a particular kenogram:
To return to the previous example where the morphogram �represented the two logical functions "&" and "" we
have:
[ (00); (01, 10, 11)] =
F(�;)
which is, of course, nothing else but a representation of the set of the inverted logical functions "&" and "&":
[ (00); (01, 10, 11)] =
F1(0,1) = (&)
-1
[ (00); (01, 10, 11)] =
F2(1,0) = ()
-1
From these remarks the general,, invariant, definition of a morphogram M can be deduced:
( i
� j
� k
� ...
� l) = 1,2,... m
n
Nevertheless, for practical reasons it is advantageous to stick to a standard sequential arrangement of the independent variable X
n which is most easily accomplished by associating with each combination of values 0
� (m - 1) of the n elementary variables x
0 � x
n-1 a digital number with basis m:
and by ordering the sequence of kenograms in a morphogram according to ascending values of the independent variable
If this convention is adopted, morphograms may be written as a sequence of symbols~the kenograms-whose position in this sequence uniquely defines the independent variable's value associated with this kenogram.
It may be useful to demonstrate this ordering principle by writing all morphograms that can be written in a two-valued logic (m = 2) constraint by two independent elementary variables x
0, x
1 (n = 2):
The detached left table indicates the adopted sequence of values in the independent variable in binary form through x
0 and x
1 and in decimal representation, headed by N.
The right-hand table gives the various possible morphograms that admit at most two different values, with numbers at the top of the table (1, 7) indicating the number of morphograms that can be obtained when precisely one, or precisely two, different values are admitted to occur in a morphogram.
I believe that the quickest way to see how many morphograms can be written that admit precisely k values in a system that has n elementary variables and m values is to look again at the inverse representation of logical functions:
Since in such a system we have m
n distinguishable "objects," these are the different values of the variable X
n and k indistinguishable "cells" which represent the k inverse functions
*3) Fk, our problem is translated into the
problem of finding the number of ways in which m
n distinct objects can be distributed into k cells, no cell empty. The answer to this question is, of course, a well known result in elementary combinatorics
[42]. Let N(n, m, k) denote the number of morphograms that admit precisely k values in a system with n variables of m values, then
where S(N, k) are the Stirling Numbers of the second kind
[53]. The number of morphograms in such a system that admit at most k values, consequently is
and those that admit the full range m of the value possibilities (k = m):
If we restrict ourselves to two elementary variables (n = 2) we have
the numbers of which are given below for the first four values of m:
Referring to the example given earlier, in the simple case of a two-valued logic, the number of morphograms is
N(2, 2) = S(4, 1) + S(4, 2) = 1 + 7 = 8
This appears to be a trivial result for this number can be directly obtained if one realizes that each morphogram admits only two interpretations, namely one function and its negation by replacing the values of "0" and "1" with their complements "1" and "0," respectively. Since there are only sixteen logical functions, half of which are the negations of the other half, the number of morphograms is clearly 16/2 = 8. However, I believe I am correct in saying that in general, for m > 2 and n > 2, a morphogram represents precisely all those functions which can be generated from one represenative function by a cascaded application of m-valued negators. In other words, a morphogram represents the logical strilcture of a particular function plus all its negations.
GOTTHARD G�NTHER: Von Foerster is right: a morphogram represents indeed the logical pattern of an individual function together with all its proper negations. It is important to lay stress on the term "proper." During the first attempts to utilize many-valued systems of logic some ad hoc devices have been introduced which were improperly called "negations." We here abide by the traditional or classic concept of negation where negation is a symmetrical exchange relation between two values. If we have at our disposal a string of values m which belong to an m-valued logic, then we possess m - 1 independent negations Neg
i where each negation of a given value produces an exchange relation with the immediate successor-value. This yields the following generalized table of negations for m-valued systems:
It should be pointed out that it is quite irrelevant for kenogrammatic purposes which of the string of values that may be inserted into a morphogram is called positive and which is called negative. The only thing important in the present context is that a morphogram is a structural feature which remains invariant with regard to negational operations in traditional or many-valued logic.
But Von Foerster's analysis of kenogrammatic structure must elicit an additional comment: in connection with his table M, he speaks of an apparent triviality of the morphogrammatic concept. However, there seems to be another triviality hidden in the very same table. It contains only familiar structures, albeit we are told that if the white triangles are occupied by a given value, the black triangles permit only occupancy by a different value. It is unfortunate that in the special case of a two-valued logic the number of morphograms is exactly eight and the number of value sequences in a table for so-called binary truth functions is sixteen. This points to a symmetry of structure which has been frequently noted in the history of traditional logic. The apparent triviality of the concept of kenogrammatic structure, however, disappears if we notice that the detached right table uses only two kenogrammatic cases � and whereas the range of N is 0, 1, 2, 3. In other words: the detached right table is "morphogrammatically" incomplete. Its four-place sequences permit the introduction of two additional kenograms. They will be represented by two new symbols, a square

and a diamond
; and in order to indicate that they represent our entrance in trans-classic structures of logic we give them a common feature by putting diagonals in both. We are now able to complete table M by adding M
t
I call the sequences in the second table
M, in order to indicate that they represent the trans-classic realm of the kenogrammatic system for the special case of four-place sequences. Both tables together constitute what has been called in the earlier paper "trito-structure".
Deutero-structure and proto-structure are then easily obtained by a process of "kenogrammatic abstraction." First, the actual location of a kenogram within a given sequence is deemed irrelevant. If one sticks to the paradigma of four-place sequences, the first abstraction yields five partitions within the trito-structure. I have visibly represented them in TABLE 2 of my formal paper read by arbitrarily choosing one morphogram of each class. The result of this abstraction was called deutero-structure. For the transition to proto-structure a different concept of abstraction was employed: in trito-structure as well as in deutero-structure, there are no limits for the iteration of a given kenogram. In proto-structure iteration will be permitted only for the purpose of completing the stipulated length of the morphograms. For this purpose the iteration of a solitary kenogram is sufficient. The individual shape of the kenogram that is chosen for iteration in order to make the structure "visible" is, of course, irrelevant.
Since our universe displays a temporal pattern, and logic is supposed to provide us with a rational description of the code of the universe, it is obvious that a computable connection between "timeless" logic and Time has to be established. However, since the computing process of consciousness displays its own temporal features it is impossible to introduce time post festum into logic. Time can always be eliminated from all systems of logic whose very basis does not already involve structures amenable to a temporal interpretation. If Time is introduced post-natally, its features can always be substituted
by features of logic of nontemporal character
[64].
Since classic logic uses only two ontological loci, called in epistemology "subject" and "object," the paper on "Time, Timeless Logic and Self--Referential Systems" proposed a third ontological locus for Time to be incorporated in the very basis of logic. If we want to speak in the now rather obsolete language of values, this would call for a three-valued logic. But the introduction of a third kenogram leaves us with a morphogrammatically incomplete basis, since classic logic already uses four-place sequences. Thus, another kenogram was, required and my formal paper showed why we should be at liberty to introduce an indefinite number of kenograms.
The very purpose of our presentation of the kenogrammatic structure is to show value systems of logic so to speak in their pre-natal state from which logic emerges after values are introduced and are ready for insertion into individual kenograms. It was important to show that there is such nontrivial structure which is indifferent to negational operations, since negational operations belong to the very core of value systems. And in order to make a philosophic concept noneliminable from value systems of logic, this very concept has to be introduced at a level where values are still irrelevant.
This we did with the concept of Time. It will now be our task to show that the kenogrammatic structure displays certain features which easily suggest temporal connotations.
It is obvious that the kenogrammatic structure may be analyzed in two different ways. We may either read TABLE 2 of my formal paper in a horizontal or in a vertical direction. In the first case we compare kenogrammatic sequences of equal length but of different structure; in the second case we compare shorter sequences of kenogrammatic symbols with longer ones. This leads to two logical concepts which can hardly be divorced from temporal connotations. Both concepts date back to a certain ambiguity in Plato's theory of Ideas, which led to the famous controversy between Xenocrates and Speusippos. Their common problem was the time structure of reality. We shall not delve into the subtleties of the debate. But from it two distinct ideas about the history of the universe have evolved.
[75] One can either assume that at the Grand Beginning everything that later become actual appearance was already extant and the temporal process is nothing but an unfolding and gaining distinction of something which rested before Time began in the gray Neuter of a primordial substratum. The other assumption is that the multiplicity of things of the real world did not have a primordial pre-existence in some mysterious metaphysical essence but came into being only gradually by the development of more and more complex structures.
The first concept is called "emanative" and the second "evolutive." The controversy as to wnether the history of the universe is to be considered as emanative or an evolutive process is as old as the history of science, and the controversial arguments seem to be far from exhausted. Some thinkers have suspected that what we might call the time structure of the universe is a compromise between emanative and evolutive principles. But their arguments have never been convincing, because they were defeated by the logical complexity of their problem.
Since the terms "emanation" and "evolution" were never well defined in formal logical terms, it was a hopeless task to try to understand the history of the universe as an interplay of an emanative and an evolutive component.
We shall have no pre-conceived ideas about evolution and emanation. We merely stipulate that we shall call the logical relations and concepts which arise from the comparison of kenogrammatic sequences of equal length "emanative" and those that the comparison of kenogrammatic symbol sequences of nonequal length yields "evolutive." If it happens that some of our statements about both time structures agree with the statements of the philosophers of history, we shall consider this a pleasing and gratifying coincidence. But as far as they do not agree, we like to point out that we do not consider emanation and evolution as mysterious processes with properties per se. Exactly the contrary is the case. We stipulate certain properties and say afterwards: This is what we call "emanation," and that is what we call "evolution." In fact, we have already done so by labeling the relations between shorter and longer kenogrammatic symbol sequences "evolutive," and the relation emerging from the horizontal order of sequences of equal length "emanative."
We shall confine ourselves here to discussing one issue that is closely linked to the controversy about emanation and evolution. The issue centers in the much debated question: Is the temporal process of the universe goal-directed or not? We know from our experience that certain systems in the universe display a goal-directed behavior but others do not. But what about the universe as a whole? The question is not merely metaphysical. It is of practical importance for the understanding of the behavior of living systems.
To obtain an answer to this question, we shall first investigate the "vertical" relations between shorter and longer kenongrammatic sequences. We shall use the method of mapping and intend to demonstrate it within the vertical relations of deutero-structure. If we map every kenogrammatic sequence unto itself, we shall find that such a mapping process either yields the same kenogram or one of shorter length. What cannot be done is to map a kenogrammatic sequence unto itself in such a way that a shorter kenogrammatic sequence may produce one of greater length.
In order to show the method in some detail we introduce two new concepts which we may call "monomorphy" and "kenogrammatic equivalence."
[86] A monomorphy is the set of all iterations of an individual kenogram. The boundary case of such monomorphy is a single kenogram. It is irrelevant whether a monomorphy is interrupted by one or more kenograms of different shape. It is only for the purpose of a simpler demonstration that we are going to write our monomorphies below in uninterrupted sequences.
Two kenogrammatic sequences are keno grammatically equivalent if they show the same structure but different kenogrammatic symbols are used. Thus, the sequences �� and � are equivalent. However, the sequence � is not

equivalent with the two preceding ones.
Since our mapping process, although permitting the interruption of a monomorphy, does not allow its breaking up for mapping purposes, we find that the five kenogrammatic sequences with four places represent the preceding shorter sequences in a way which is shown diagrammatically in the following table:
Inspection of this table shows that the monomorphy with four places, if mapped unto itself represents only itself. The next sequence exists of a threeplace and a one-place monomorphy. The arrow points to the three-place and one-place sequences which results from the respective mapping processes. The reader should not be confused by the fact that the one-place monomorphy at the bottom contains a dark triangle and the one at the top a white triangle. Both are kenogrammatically equivalent and this is what counts. The third kenogrammatic sequence at the bottom is composed of two two-place mono-morphies. Owing to their equivalence both represent the monomorphy to which the arrow points. The next kenogrammatic sequence at the bottom is formed by a two-place monomorphy and two monomorphies of once place. This permits a much wider representation by the mapping process as is seen in the diagram. We remark, incidentally, that equivalent monomorphies are always shown with one set of symbols only. The choice of the symbols is principally free, but since we use in two-place sequences only triangles, the image of the sequence

is represented by �.
The last kenogrammatic sequence is composed of four one-place monomorphies. It may, of course, be mapped unto itself in such a way that either one or two or three monomorphies are eliminated. Thus, this four-place sequence like the preceding represents three-place, two-place and one-place sequences.
The letters I, O, C at the bottom of this diagram represent the terms "Incomplete," "Overcomplete" and "Complete". If a four-place sequence does not represent all preceding lengths of sequences, the representation is said to be "incomplete"; if it represents all preceding lengths but any given length in more than one way, it is called "overcomplete"; and if it shows for each length one example of representation it is "complete." It should be noted that this classification of the demonstrated mapping capacities is not exhaustive. In order'to make it so, we have to assume another case which shall be called " para-complete." A representation is said to be para-complete not if all preceding lengths of kenogrammatic sequences are representable by the mapping process, but rather if a given length could be represented twice. This case, which makes these representational distinctions exhaustive, however, occurs only if kenogrammatic sequences with eight places are introduced.
One should be aware of the mapping relations being unidirectional. The four-place sequences are, in our case, the domain of the mapping procedure and the shorter sequences represent its range, but not vice versa. It follows that, as far as the history of the universe is exclusively governed by evolutive principles, the future is unpredictable. And it is unpredictable for purely logical reasons; in other words, it is not empirical unpredictability, which may be removed by sufficient accumulation of data-it is an a priori unpredictability. The evolutive structure permits only a look into the past. In this context we may recall that Plato says all knowledge is recollection (anamnesis).
Considering its logical structure we cannot assume the evolutive process to be goal-directed. It tends towards greater and greater diversity without an ultimate principle of integration.
Now we turn our attention to what I have called the emanative structure. I shall use for demonstration the trito-structure with kenogrammatic sequences of four places. The very same concept of mapping will be applied. But since this operation is now concerned with relations between symbol sequences of equal length, the mapping procedure demands that monomorphies may be split up. Two examples shall illustrate the idea.
A morphogram iterating a single kenogram over all four places is mapped onto itself. The arrows indicate the mapping method. The results show in both cases that the four-place monomorphy is broken up into a three-place and a one-place monomorphy. It stands to reason that several mapping procedures are available to obtain the very same result.
Starting from the opposite end of the trito-grammatic structure we might start the mapping as follows :
In the past example, a morphogram with four one-place monomorphies is also mapped onto itself; the mapping method is again indicated by the arrows. This yields, as we see, again a four-place morphogram which consists of two one-place and one two-place monomorphies. The examples show that this time the mapping process can be applied in both directions. If we proceed from left to right the kenogrammatic iterations decrease from four places to one. But while this happens, the number of kenograms increases. If we proceed from the right to the left, the number of kenograms decreases, but the iterative capacity of the remaining kenograms increases. Displayed in a diagrammatic form, the pattern looks as shown on the next page.
The dotted line represents the decrease, or increase of iteration; the dahsed line the corresponding increase or decrease of kenogrammatic differentiation. Since the mapping process permits a start from the maximum of iteration as well as from the maximum of differentiation, the emanative process is-judged by purely logical principles- predictable. Moreover, whereas the evolutive process (which may be demonstrated either with proto-, deutero- or tritostructure) is only one, there are many emanative processes as we can count logical stages of evolution. The emanative processes are always finite, but they are of different length. Their length depends on how many iterations are permitted for a solitary kenogram.
It is interesting to note that medieval philosophy decidedly preferred the emanative pattern of world history. Since the history of the universe begins with the creation (and Paradise Lost) and develops towards the Last Judgment (and Paradise Regained), this temporal process is finite as well as goal-directed.
If we want to draw a corresponding pattern for evolution as we did for emanation, it would have the following shape:
The horizontal line of crosses extending into infinity in both directions represents the unlimited potentiality for extensional structure. But out of the infinity of available starting points (+) for evolution, one individual ontological locus (�) is singled out: the logical pattern begins with a solitary kenogram. From here the structure gradually broadens out into a potentially infinite diversity. But the later logical structures are not contained in the solitary kenograrn which represents the beginning. They are a result of structural relations generated by the subsequent diversity. In other words, the philosophical category of the "New" is germane to the evolutive pattern of thinking.
On the other hand, there can be nothing new in a process which follows solely emanative principles of development. For the emanative thinkers the history of the universe is a gradual appearance of what there already is. John Scotus Eriugena (810-877 A.D.) describes the universe as a theophany, i.e., a revelation of God during the progress of Time.
The modern thinker dealing with temporal structures is, of course, preponderantly interested in the issue of scientific predictability. We have noted that the evolutive pattern excludes predictability a priori. The emanative pattern not only permits predictability, it even implies it logically. But since everybody knows that in our world certain events are predictable, the temporal process of our universe must actually be a compromise between evolutive and emanative laws. The following diagram sketches the actual
temporal process of our universe as an ideal compromise. It is, however, highly improbable that such an ideal compromise takes place in our real world. Our scientific data rather suggest that either emanative or evolutive trends may dominate.
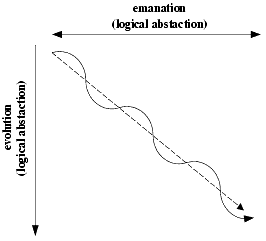
If we call logical systems which are proponderantly dominated by emanative structures "overbalanced," systems of an ideal compromise "balanced," and systems where evolutive patterns outweigh emanative structures "underbalanced"
[97] then the actual Time structure of the world we live in must be probably described by a sequence of systems which weaves incessantly from underbalanced systems to overbalanced systems and back. This, of course, implies that Time structure is influenced by the events which take place "in" Time. The popular concept of Time, where Time is visualized as a sort of clothesline extended from infinity to infinity, independent of whether the housewife clamps on her laundry or not, has been proved inadequate long ago. But so far no serious attempt has been made to connect Time with the
complementarity of evolutive and emanative structures. If we use only twovalued logic with its two corresponding kenograms, this complementarity displays only trivial properties. The classic, two-valued logic is not an adequate tool for the problem discussed above.
1. GUNTHER, G. 1963. Cybernetic ontology and transjunction operations. In Self-Organizing Systems: 313-392. Spartan Books. Washington, D. C.
2. RIORDAN, J. 1958. Introduction to Combinatorial Analysis: 99. John Wiley & Sons. New York, N. Y.
3. ANDREW, A. M. & H. VON FOERSTER. 1965. Table of the Stirling Numbers of the Second kind. Tech. Report No. 6, AF-OSR Grant 7-64, Electrical Engineering Research Laboratory, Engineering Experiment Station. University of Illinois, Urbana, Ill.
4. This has been shown for a very important instance by W. S. McCulloch and W. Pitts by their derivation of a "temporal propositional expression" in which Time does not appear explicitly, but where sequential order is provided by an iteratively employed operator S. (1943. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5: 115.)
5. Cf. W. WINDELBAND. 1928. Lehrbuch der Geschichte der Philosophie. : 203. Verlag J. C. B. Mohr. T�bingen, Germany.
6. For the concept of "kenogrammatic equivalence" I am indebted to Mr. Dieter Schadach.
7. For a more detailed account on the distinction between overbalanced, balanced and underbalanced systems of logic see G. Giinther. 1963. Das Bewusstsein der Maschinen. : 177f. Agis Verl. Baden-Baden, Germany. It should be added, however, that loc. cit. the distinction was only applied to logical systems with values.
1*) Prepared under the sponsorship of the Air Force Office of Scientific Research, Directorate of Information Services, Grant AF-AFOSR-480-64 and Grant AF-OSR 7-66.
1Ann.N.Y.Acad.Sci. 138 (1967) 874-891
2[1] GUNTHER, G. 1963. Cybernetic ontology and transjunction operations. In Self-Organizing Systems: 313-392. Spartan Books. Washington, D. C.
3*) The cells are indeed "indistinguishable," for it is irrelevant which particular value the argument y in these functions assumes. The only condition is that these values are
different from each other.
4[2] RIORDAN, J. 1958. Introduction to Combinatorial Analysis: 99. John Wiley & Sons. New York, N. Y.
5[3] ANDREW, A. M. & H. VON FOERSTER. 1965. Table of the Stirling Numbers of the Second kind. Tech. Report No. 6, AF-OSR Grant 7-64, Electrical Engineering Research Laboratory, Engineering Experiment Station. University of Illinois, Urbana, Ill.
6[4] This has been shown for a very important instance by W. S. McCulloch and W. Pitts by their derivation of a "temporal propositional expression" in which Time does not appear explicitly, but where sequential order is provided by an iteratively employed operator S. (1943. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5: 115.)
7[5] Cf. W. WINDELBAND. 1928. Lehrbuch der Geschichte der Philosophie. : 203. Verlag J. C. B. Mohr. T�bingen, Germany
8[6] For the concept of "kenogrammatic equivalence" I am indebted to Mr. Dieter Schadach.
9[7] For a more detailed account on the distinction between overbalanced, balanced and underbalanced systems of logic see G. Giinther. 1963. Das Bewusstsein der Maschinen. : 177f. Agis Verl. Baden-Baden, Germany. It should be added, however, that loc. cit. the distinction was only applied to logical systems with values.

have:
and a diamond
; and in order to indicate that they represent our entrance in trans-classic structures of logic we give them a common feature by putting diagonals in both. We are now able to complete table M by adding Mt
equivalent with the two preceding ones.
is represented by �.
