Gödel Games: "Cloning Gödel's Proofs"

It comes, maybe, like a call from hell, that the only book in the Google-print universe in which my name is mentioned, is Kurt Gödel, Collected Work, Volume IV, Correspondence A-G edited by Charles Parsons et al. The occurrence of my name is in straight order: Gödel, Günther, Kaehr. Gödel-Günther, the Correspondence. My name in the bibliography of Gotthard Günther, mentioning an appendix to Idee und Grundriss, second edition 1978, my PhD dissertation.

There was probably also only one review of Grundriss+Appendix, mentioning this complex a dinosaur. Günther's work the body, the appendix its tail; what else? Both boring, not even contributing anything to the linguistic turn, but, at least, you could jump from one boredom to another catastrophe.

Now, after all this movements have disappeared: linguistic turn, analytic philosophy, modal logic, deconstructivism, second-order cybernetics, critical rationalism, critical theory, radical constructivism, holism, system theory, etc., time may be ready to read Günther, and especially the Gödel-Günther Correspondence, again, or for a very first time.

Wouldn't it be beautiful if we could celebrate Gödel's proofs in disseminating them over all universes and contextures we know until now without getting blocked into the monolithic character of negative fundamentalism we are confronted in established understanding of Gödel's limitation theorems? Couldn't such a dissemination celebrate its ultimate universality even to worlds which had been profoundly disturbing Gödel? Like Günther's multi-verses and other kinds of discontexturality?

Cloning the naturality of natural numbers is still the program of DERRIDA'S MACHINES.

Cloned objects are more beautiful than natural objects because they originate in a mundane context, not being obscured by extra-mundane sources.

Iter as accretion in distributing the same functor over poly-contexturally different contextures.

Iter as reflection is introspecting the same functor over intra-contextural ranks of a contexture.

Iter as interaction is disseminating the same functor over trans-contexturally different contextures.

"Q equals a completely known 3-character string. Our presentation of Gödel's argument was parallel to his, but using strings instead of numbers.The heart of the argument is a transformation from one level of quotes to two levels, and back down to one, with a "¬" appearing in the process. We can simplify the argument without loss of content by going from zero to one and back. So are the properties necessary to make the argument: a theory must allow us to replace something with its equal, and it must include or allow us to define its own interpreter. To save such a theory from inconsistency, we could suspend the ability to replace something with its equal under certain circumstances, but that is a distasteful option. Instead we leave the interpreter incomplete. In particular, if "¬ I Q " = ¬ I Q is a theorem then we have inconsistency, and if it is an antitheorem then I is not an interpreter, so we leave it unclassified." Hehner

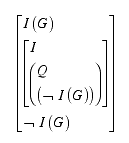"In this situation "I can not unquote "¬ I G "" because it would produce a contradiction, which would be fatal for the interpreter. In this sense, strict self-referentiality is excluded. To save such a theory from inconsistency, we could suspend the ability to replace something with its equal under certain circumstances, but that is a distasteful option. Instead we leave the interpreter incomplete. In particular, if "¬ I G " = ¬ I G is a theorem then we have inconsistency, and if it is an antitheorem then I is not an interpreter, so we leave it unclassified." Hehner

But this situation makes sense only for a mono-contextural framework. In a poly-contextural setting with its distinction of identity/sameness, the formula can be unquoted by change of contexture without producing a conflictive contradiction in the complex system. And the "unclassified" situation can be given a positive meaning and an own logical status in a different logical system. Thus, self-referentiality can be handled without contradiction in a poly-contextural language. And the same for contradiction. Contradiction in one contexture can be modeled, quoted as a contradiction, in another contexture without producing a collapse of the logical system as a such.

Incompleteness seems not to be as distasteful as to suspend axioms of equality to save the system. But, for systematic reasons, both are structurally equal. Thus, equal distasteful. Again, incompleteness and not being classified, enables the illusion of some freedom of choice. But it is only the other side of the coin, therefore a question of taste not necessarily of thinking.

Inconsistency is depending on negation or its equivalents. Polycontextural logics are multi-negational systems, thus, the notion of inconsistency is changing. It seems that inconsistency becomes a special case of incomparability.

In this small game of quotation/interpretation interesting terms are involved: contradiction, self-referentiality, incompleteness and unclassified. Quite substantial stuff for a theory of computation. The emphasis is optimism, interpreting negative results positive; negative teleology.

Compare the result of the substitution with the start postulation of the procedure.

Quotations are logical sentences like all other logical sentences too. They can be evaluated to the value true or the value false. E.g. Eval(Quote(true)) = true.

The defined theory "allow us to replace something with its equal" but it is not able to disallow a distributed substitution because equality of terms is defined in the theory only "up to isomorphism". Such theories are identifying the terms "equal" with "same". The polycontextural approach offers a different option to the difference of equality and sameness. Equality in this sense is an intra-contextural term but sameness is a trans-contextural term. Because substitution is generally defined in a theory only up to isomorphism we always have the possibility to interpret the action also in a trans-contextural way. As long as the definitions of the theory are not disallowing this way to use substitution there is always some degree of freedom to interpret the terms in another similar theory. In other words, in a polycontextural situation a substitutional action has to decide if it is of intra- or a trans-contextural kind. In a highly complex situation it is even possible that both kinds of substitutions are reusable at once and that the trans-contextural substitution can even be distributed over several neighbor theories instead of only one.

Thus, the formal conditions for this new game are: non-characterizablity ("up to isomorphism") of the action or relation of substitution and polycontextural distribution of formal systems.

Obviously, the terms or formulas which have to be compared have to belong to the exact same, i.e., identical formal system. Between the steps of the development of the equation there is now jump to another system. This is guaranteed by the strict identity of the terms and the equation relation. In other words, transitivity of the equation relation holds strictly.

"We believe that our presentation of Gödel's Incompleteness Theorem(s) nicely illustrates E.W.Dijkstra's contention that computing science can now repay with interest its debt to mathematics. Specifically, the distinction between program and data, the use of the character string data type, the use of an interpreter, and counting from zero, reduced the proof to three lines. " Hehner, 1990, p. 6

In a polycontextural setting we are free to choose a more flexible interplay between quotation and interpretation. To quote means to put the quoted sentence on a higher level of a reflectional order or to another heterachical actional level. We are not forced to limit ourselves to any kind of the well known intra-contextural meta-language hierarchies. Those local procedures are nevertheless not excluded at all but localized to their internal place.

To start the argumentation I simply map an index i to the sentences. A quotation is augmenting and an interpretation is reducing its value, say by 1.

This setting is neutral to reflectional and interactional definitions of interpretation and quotation. It reflects the main idea that quotation/interpretation is an epistemic action and is therefore, from a polycontextural point of view, involved in locating its propositions into the contextural grid of cognition.

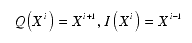
A first step to a polycontextural formalization of the quotation/interpretation mechanism is introduced with the Quotational Calculus. This calculus is modeling the quotation/interpretation mechanism along the dimensions of reflectionality and interactionality of polycontextural logics. On this level of formalization features of transjunction are not involved. Transjunctional quotation/interpretation would introduce a bifurcation into the operators I and Q allowing to operate on the sentence at once at different locations.

On this level of reflection, to make a start, we will study Gödel sentences in their singularity, involved in reflectional and interactional interpretations, but not as simultaneous multitudes, occurring at all knots of our contextural grid. But this surely, will be the real thing: Ubiquity of Gödel's games.

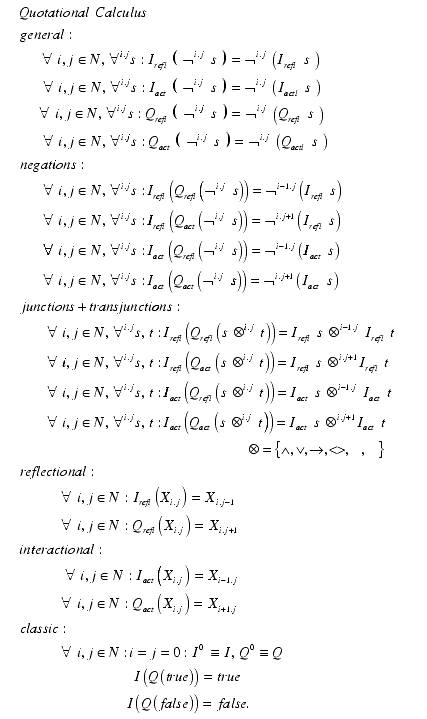
General pattern of quotation and interpretation. The terms s and t are changing their index depending on the index of the operators. To emphasize on the essentials of the construction only the relevant changes of the formula are notated.

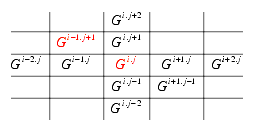
Reflectional operations are changing the index j and interactional operations the index i of the level of the tabular terms Xi.j. This has to be applied to the general rules for negations and binary operations.

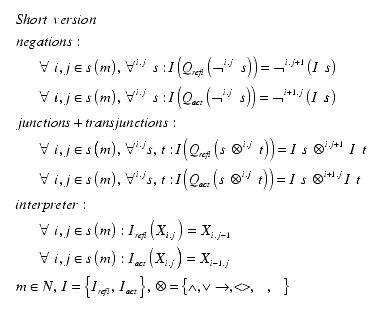
The indices are marking the location of the formula as a whole. It would be to much of notation to mark all parts of a formula with indices.

Reflectional and interactional operators, like I and Q, are defining a simple cellular automaton with the movements M={left, right, up, down} and a corresponding set of rules. OK, a tessellation of kenomic loci is surely not what Wolfram's world or Fredkin's universe are constructing, simply because they are entirely mono-contextural, preserving and guarding their Gödel sentence jealously.

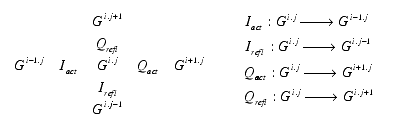
Depending on the strength of reflectionality and interactionality involved in the game, the operators I and Q can realize wider jumps inside the matrix. Thus, single operators can be seen as iterations and have not to be restricted to a pus-1/minus-1 jump. This is a further step to dynamize the game of interaction and reflection. Further, but not considered here, transjunctional constellations for quotation/interpretation would have to enter the game to make it more dis-contextural.

Despite the final meaning of Gödel's proof I focus on the operational steps, not on the what of the construction but on how it is realized. What are the strategies of Gödel's game? The meaning of the construction remains in the mind, the operations are inscribed on the wall.

"The heart of the argument is a transformation from one level of quotes to two levels, and back down to one, with a "¬" appearing in the process." Hehner

Again, there is no statement by Hehner about what kind of levels are involved. Therefore, to re-beautify or dis-beautify the Gödel construction we are allowed to involve the game into at least two additional kinds of levels: the reflectional and the interactional levels of polycontexturality. Thus, we are free to interpret the term "level". It can be, as well known, intra-contextural, representing the classic logical or computational situation. Or additional, trans-contextural, a reflectional but also an interactional strategy. And other interpretations of the modeling strategy not yet introduced, too.

With polycontextural modeling, instead of a contradiction we get a separation. The comparison happens in a third system which compares the result of system S1 with the result of system S2. From the point of view of the third system S3 it is even possible to cancel the contextural differences and to put the whole derivations with their system switches back into one and only one contexture, so we would have returned back to the mono-contextural case and produced as usual the famous contradiction. But this time we would know a little bit more about the genesis, the mechanism and the hidden conditions of this contradiction, not by supposition and intuition but by construction.

In all cases, the wording of the modeling has to be preserved. There will be no change of the pre-given formulations. Neither in the definition of the problem nor the procedure of its solution. What differs only are the possibilities of interpreting the notions involved. In the classic case there is no space for different but similar (analogues) thematizations. But this new possibilities, again, are in no violation to the pre-given notions, because these notions are simply not defined in strict non-ambiguous terms, thus giving space for legitimate deviations in the frame of preserving analogies.

With the classic setting there is a asymmetry between quotation and interpretation. Formulas have to be interpreted by I. A quoted sentence is "passive", like a stored program, an interpretation I is activating the passive sentence and changing it into an "active" one. "That is what an interpreter does: it turns passive data into active program." (Hehner) Therefore there is an operational asymmetry between quotations and interpretations. In the polycontextural setting this asymmetry is relative to its local realization. Between different contextures, quotation and interpretation, are in a symmetric exchange relation. Asymmetric relations between quotation and interpretations are keeping at all loci they occur the Gödel results. They are repeating at each locus the Gödel configuration. Thus, they are guaranteeing the ubiquity of the Gödel sentence over all contextures.

Symmetric relations are spacing, giving space, to constructions which are not producing contradictions but analogous or queer Gödel constellations being distributed over different contextures. Thus, quotations become active. The relation between interpreter/quotation, i.e., between active and passive, is now dynammic and not a static pre-given hierarchic relation.

Obviously, we observe again an order relation between the asymmetry of interpreter and quotation, and an exchange relation between interpreter/quotation for the symmetric trans-contextural situations. And because we are dealing in all cases of the distribution with quotation and interpretation and not with something different, the coincidence relations are realized. Thus, the whole dissemination of the Gödel construction is well managed, i.e., mediated by the proemial relation.

The asymmetric constructions are directly conform with the wording of the construction. They simply have some additional indices marking their place in the contextural grid. The asymmetric constructions are accepting the wording, too. But are involved in an analogous understanding of the main notions based on the coincidence relations of the dissemination.

Based on the passive/active chiasm, it seems, that we have now two possibilities to deal with the Gödel sentence. One needs an interpretation I of the formula, the other is dealing directly with the formula. The first uses the passive understanding of the quotation and needs an active operator, the interpreter I. The second is based on an active understanding of the operation of quotation Q and is able to deal directly with the formula. The activity of the quotation operator is to shift the formula to another level, while the activity of the interpreter is to reverse this shift. As long as we don't use indices to mark the different contextures the mechanisms coincide.

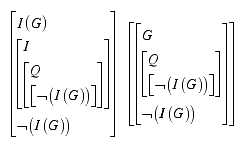
In other words, what is an interpretation in one constellation is a quotation in another, and vice versa. Quotation in a polycontextural constellation is not freezing a statement in contrast to the activation of the interpreter. Both operators are in a dynamic interplay.

As a result of the distribution of the Gödel sentence and the new dynamics between interpreter and quotation we have to distinguish at least two new features:

1. MULTI-VERSAL UBIQUITY of Gödel, i.e., multi-versal validity and availability,

The interactional interpretation of iteration is distributing the formula over different contextures, still in accordance with the primary wording of quotation and interpretation.

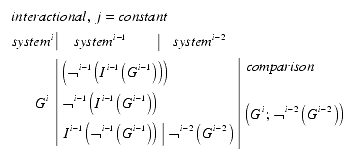
The first part of the bracket formula shows an interactional realization of the Gödel sentence, repeating it at the locus i, producing not a contradiction but incomparability. The second part realizes a shift further to another contexture, producing more distance to the original position.

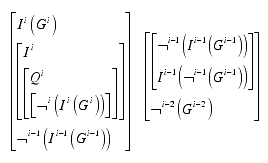
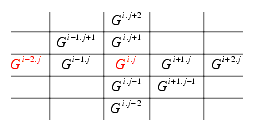
This horizontal distribution of the Gödel sentence shows a save interactional distance to its original sentence without any detours.

Like the interactional, the reflectional interpretation of iteration is distributing the formula over different contextures, still in accordance with the primary wording of quotation and interpretation.

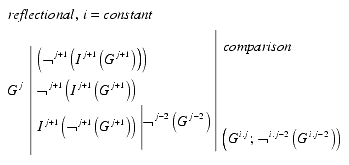
The first part of the bracket formula shows an reflectional realization of the Gödel sentence, repeating it at the locus i, producing not a contradiction but incomparability. The second part realizes a shift further to another contexture, producing more reflectional distance to the original position.

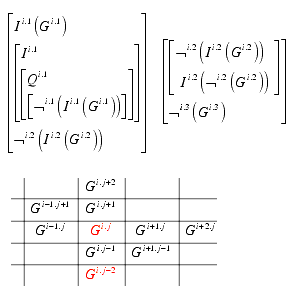
This vertical distribution of the Gödel sentence shows, dual to the horizontal, a save reflectional distance to its original sentence without any detours.

Quotations are reflectional or epistemic attributes (operators) and not semantic attributes like valuations with true and false.

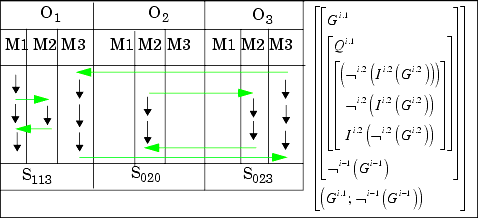
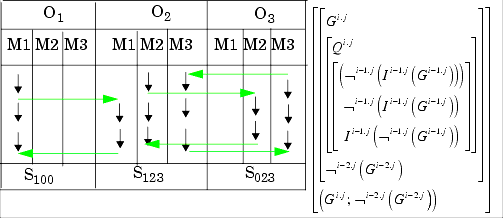
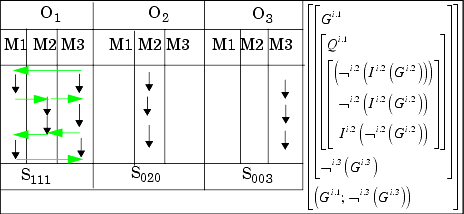
The construction starts in systemi.1 (in the diagram at O1M1=S1.1) by decision, then reflects and maps it inside of systemi onto systemi.2 (O1M1 to O1M2) and interacts in a next step with systemi-1(O2M2 to O3M2). The comparison of the two results, the beginning and the end of development, (Gi.1, noni-1Gi-1), has itself a representation in systemi-2 (O3M3 to O1M3). This development is achieved by applying a reflectional interpreter Ii.1 and a interactional interpreter Ii.j+1 successively. Obviously, the resulted comparison has not produced any contradiction. But nevertheless some kind of "deep-structure" of a contradiction is preserved: we only have to cancel the notation of locations and dislocations, that is, the indices, to obtain our well known contradiction. Thus the structure of the construction is mapping the contradiction in its behavior but not in its semantics. The comparison as an incomparability can now be studied in its own contexture, say systemi-2. A first step can be to ask about the distance between the compared sub-systems and how this distance is characterizing the whole system as such.

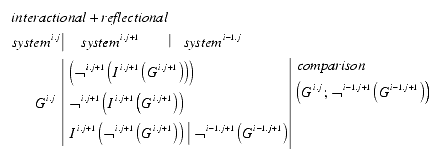
Mixed behaviors, interactional and reflectional, are producing, additional to the strict horizontal and vertical moves, some diagonal behaviors. Diagonal strategies are open up rules for stronger distance or strangeness to their origin. Some loss of simple safety in distance is involved.

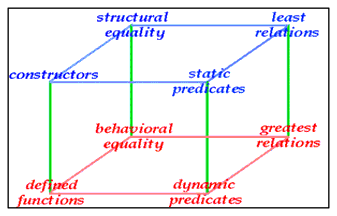
Semantics/Meontics are per se static, that is, structural and algebraic systems. Well described by algebras, governed by equality relations as their criteria of equality.

These semantic formulas are hinting to the semantics of PolyLogics. Locally, each logic can be considered as a 2-valued system, here, with strict classic negation rules between truth and false. The pairs of truth-values are connected to a chiastic chain ruled by the proemial relation over the truth-values and their loci. The chain may be structured by more complex architectonics then linearity.

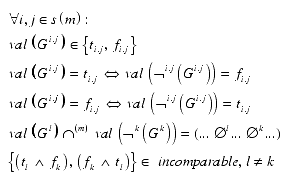
Because of the incomparability of systemi.j and systemi-2.j for example, no contradiction can happen. No contradictions for the interactional, reflectional and mixed strategies; only some sort of incomparability or incompatibility, but a lot of additional clean intra-contextural contradictions.

Incomparability can be studied per se and also in their relation to the system they occur. Logical contradiction, thus, is incomparability with zero distance, is otherness with zero tolerance.

Polycontextural semantics, understood as meontics, will have to deal not with logical truth and falsehood, in Tarski's or Kripke's or others sense, this may still be preserved locally, but with new constellations of strangeness, closeness, distance to otherness and togetherness and their epistemological topologies.

"An adequate truth theory for a language defines the language and determines the set of its tautologies. It does so by specifying (recursively, in a metalanguage) truth conditions for its sentences. An adequate theory of rational belief systems for a language also defines the language and determines the set of its tautologies. It does so by specifying (recursively, in a metalanguage) the conditions under which a truth or falsity claim concerning sentence of the language may be incorporated into a rational system of beliefs of the language. More briefly, we may say that it does so by specifying acceptability conditions. The difference between truth and acceptability semantics thus reflect different analyses of understanding. On one analyses, to understand a sentence is to know what would make it true. On the other, it is to know what makes it acceptable." Brian Ellis, Rational Belief Systems, 1979, p.viii

To be concerned about the truth of sentences like the Gödel ones, can be considered as an intra-contextural business. Locally, this is a crucial point, globally, in the game of poly-thematism, it is one of the stops of a wild journey. More interesting than the truth preserving/violating results in proof situations seems to be evolved by the strategic ways, the pathways discovering labyrinthine worlds, of the behaviors in the tabular game of a multitude of constellations. Depending on the complexity of the formula, different choices for reflectional or interactional thematizations of the operators, quotation/interpreter, are possible. Some kind of zag-zagging through the tabularity of the contextural grid emerges. Further more, many Gödel games may start at once at different locations. These paths of behaviors are not to be studied by their truth-semantics but by their behavioral characteristics. The method to apply is the co-algebraic study of bisimilarity. Thus, truth-semantic considerations are structural, algebraic and visible, behavioral features are co-algebraic and hidden.

A Gödel sentence can be placed at all loci of a contextural grid. Thus, we can start our game at any of these locations, in isolation or all at once, or mixed, invoking a quite wild parallelism of Gödel games.

A starting sentence like Gi.j can give opportunity for multiple thematizations at once, leading to distributed results and distributed comparisons based on a single beginning. More liberated multiplicity enters the game with the possibility to distribute the very beginnings, leading to separated comparisons in the common matrix. This has not to be restricted to separated parallelism but can introduce interwoven behaviors of Gödel games.

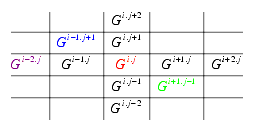
A new undecidability enter the game with the strategic behaviors of Gödel games. Truth functional strategies are visible, behavioral strategies are hidden. The method to study the behavioral aspects of a system are given by the apparatus of co-algebra. There is no recursive mechanism to follow the pathway of strategies in Gödel games. The switch from one contexture to another is not recursive but spontaneous.

Thus, additional to the different truth semantic and acceptability conditions of the structural approach, which is based on constructors, questions of comparability and equality of strategies have to be focussed. What is the criterion for the equality of strategies? An answer may be given by the notion of bisimulation.

To a user, again, the state may remain hidden, it is irrelevant, as long as the automaton implements the desired regular expression. Again, two states may be identified, if they behave the same way on the same input, which is to say, if they cannot be distinguished by any observation." Peter Gumm

The local/global game is not the end of the chances. We can thematize the whole interplay of algebraic and co-algebraic features. Both at once. Which is: total acceptance. This approach is covered by the Swinging Types, introduced with much dynamics by the German computer scientist Peter Padawitz.

Swinging Types provide a specification and verification formalism for designing software in terms of many-sorted logic. Current formalisms, be they set- or order-theoretic, algebraic or coalgebraic, rule- or net-based, handle either static system components (in terms of functions or relations) or dynamic ones (in terms of transition systems) and either structural or behavioral aspects, while swinging types combine equational, Horn and modal logic for the purpose of applying computation and proof rules from all three logics. Peter Padawitz

Also algebras and co-algebras are defined as dual conceptions and are delivering interesting results exploiting this duality and symmetry, there are also highly interesting asymmetries to observe delivering even more interesting results. One of these topics is bisimulation.

But the theory is not just a simple minded dual to universal algebra. Structures such as e.g. bisimulations, that don't have a classical counterpart in universal algebra, but that are well known from computer science, figure prominently in the new theory." Peter Gumm

There is a paradigm shift between algebra (constructors dual selectors, induction) and co-algebra (observators, co-induction) disturbing the duality between algebra and co-algebra.

What is left is the dynamics as such realized by the swinging types. The switch from static to dynamic models, from algebraic to co-algebraic and back is neither algebraic nor co-algebraic. It is neither visible nor hidden. This structure of neither-nor, total rejection, is inscribing a form beyond known scriptures of algebraic or co-algebraic character. These forms has presentations as morphograms, and is studied in the adventures of morphogrammatics.

Morphogrammatics is thematizing the very patterns of the behavior of Gödel games, abstracting, i.e., subversing the modi of their thematizations as formal systems and inscribing as a result of such a subversion the pre-semiotic dynamics of its placing, i.e., its locations, its loci, its chora.

New topics of meta-theoretical studies emerge. To each proposed approach we have to study the topics analogue to the classic questions of truth, decidability, consistency, etc. in the light of a new design of formal systems and computation.

Jumping between trees creates new forms of undecidability, new kinds of unpredictability as liveliness. Liveliness is the new kind of undecability in complexions of formal systems. Liveliness is not a loss of control and security but a guaranty of viability.

The rule that a quotation shouldn't be changed by the quoter is reasonable only for limited cases, like legally relevant quotations. But self-referential computing systems are not to be restricted by this metaphor of legality but should be more based on the metaphor of living systems. Life is not only repetition but also change, and change is not equal destruction and chaos but creative transformations.

In the terminology of Graphematics and DiamondStrategies, attributes of sentences are decidable or nondecidable. They belong either to the position or the opposition locus of a diamond. Polycontexturality is not based on sentences (propositions, statements) but on textuality and its reflectional deepness and interactional broadness. The distance of textual constructions, say in Gödel games, can be reflected as a neither-nor situation in respect of decidability and nondecidability. Two Gödel games which don't coincide have a distance, are separated and in some sense incomparable. Each Gödel game has its own Gödel sentence, thus its own distinction of decidable/nondecidable sentences. This situation takes place at the both-at-once locus of the diamond.

Thus, additional to the classic hierarchy of decdability, a heterarchy of neither-nor- and at-once-situations have to be studied.

To find back home to our story, we have to restrict and focus ourselves again on an extremely narrow game.

The whole Gödel construction lives from the fact that it doesn't leave its contextural box. It is boxed strictly inside of a contexture and remains mono-contextural despite some meta-theoretical detours. The paradoxical result is that the box is open exactly when the box is closed. And this, obviously, is in strict conflict with the underlying logic.

Inside of a polycontextural scenario, reflectional, interactional or mixed or neither-nor, there is no strictness which forces to the Gödel results. They simply belong to another world of thinking and formalizing. And by the way, this world was not even Gödel's own paradise, he always tried to surpass it. But how? Gotthard Günther has given him some hope, evoked some kind of an ultimate resolution, but at the end he/it was to late...

In the Gödel case the comparison of the results of the formula are producing a logical contradiction, the polycontextural demonstrations are showing no contradiction but only incompatibility/incomparability and separation of the parts of the formula in question. This is by no means only a negative result! We easily can deal, that is thematize, this result in an own contexture and produce some further results about separability and incompatibilities of our construction, leading to new insights about the relationship, say of a program and its interpreter in self-referential situations.

There is for sure nothing wrong with Gödel's results. From a polycontextural viewpoint there is no criticism to add, they are simply loosing their relevance for trans-computational argumentations and constructions.

Ubiquity is not universality nor naturality, it is much more, more than Gödel was able to dream: Gödel is everywhere, even in worlds which are not allowed to exist in Gödel's paranoid Platonism. There was only one other world allowed, the one where he could meet Adele again. Multi-verses would have foild his desire. Now, multiverses of any complexity are inhabited by Gödel’s Ghost. The price he paid is the loss of his relevancy. There is nothing ultimate anymore. He is a ghost as many others, too.

We have not only the joy to clone Gödel but also, and this is even more intriguing, the fun to clone Gödel's Ghost.

Like paradoxes, antinomies and all kind of contradictions and other monsters, Gödel is domesticated and has his cards to play, as anybody too. The wine of negative speculations is thin and old. To celebrate human creativity exploiting Gödel's negative results is obsolete. What we need is an understanding of creativity and computation beyond positive and negative attitudes.