On Chinese Mathematics
"Chinese culture lack formalization system like as Euclidean geometry, the circumstance disadvantages modernization of Chinese sciences, as well as modernization of technology and industry. The role of Combinatorics in the age of computer-web-information is the same as the role of Euclidean geometry in Industrialization. According to Constructivism mathematics, we believe and accept one mathematical object does exist if and only if we can construct it or build it in practice. So only parts of knowledge that have devised from manipulating the integers are truthfully reliable! " Steve Han (Jinan, ShanDong)
http://hanxianping.blogchina.com/886414.html
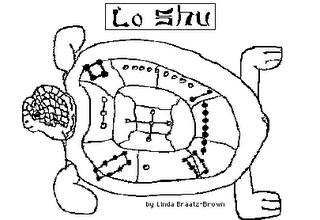
Magic Square in Lo Shu
(1)."Magic Square occurred in Lo Shu of the ancient China.
I think that represents the core of Chinese culture: Constructivism, Combinatorics. But they never become main stream culture in China." Steve Han
The story of 'Lo Shu' is as follows:
http://mathforum.org/alejandre/magic.square/loshu.html
In Chinese, the square is known as Luo Shu (Simplified Chinese: 洛书; Traditional Chinese: 洛書; pinyin: luò shū; Literal: Luo (River) Book) or the Nine Halls Diagram (Simplified Chinese: 九宫图; Traditional Chinese: 九宮圖; pinyin: jiǔ gōng tú).
http://en.wikipedia.org/wiki/Lo_Shu_Square
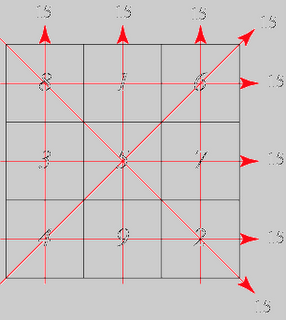
Magic Square
A magic square is a square array of numbers consisting of the distinct positive integers 1, 2, ..., n^2 arranged such that the sum of the n numbers in any horizontal, vertical, or main diagonal line is always the same number (Kraitchik 1952, p. 142; Andrews 1960, p. 1; Gardner 1961, p. 130; Madachy 1979).
Lo Shu is an associative magic square, but not a panmagic square.
(enter: Latin Square, Panmagic Square, associative Magic Square)
http://mathworld.wolfram.com/MagicSquare.html
Chinese vs. Greek mathematics
The first thing to understand about ancient Chinese mathematics is the way in which it differs from Greek mathematics. Unlike Greek mathematics there is no axiomatic development of mathematics. The Chinese concept of mathematical proof is radically different from that of the Greeks, yet one must not in any sense think less of it because of this. Rather one must marvel at the Chinese approach to mathematics and the results to which it led.
Chinese mathematics was, like their language, very concise. It was very much problem based, motivated by problems of the calendar, trade, land measurement, architecture, government records and taxes. By the fourth century BC counting boards were used for calculating, which effectively meant that a decimal place valued number system was in use. It is worth noting that counting boards are uniquely Chinese, and do not appear to have been used by any other civilization.
http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Chinese_overview.html
Axiomatic Method
Chinese mathematicians didn't develop axiomatic methods like the Euclidean axioms of geometry. It seems, that this, too, was based on a clear decision and not on a lack of mathematizing ingenuity. Chinese mathematicians had been introduced to Euclid by Westerners. They liked the concise presentation of the topics but didn't think to adopt it to their own methods.
The axiomatic method, as developed by Euclid, is based on the evidence into the "eternal" truth of the axioms and the uniqueness of the rules of deduction. Aristotle has given in his Metaphysics a decisive philosophical justification of this world-view. He defended it against the more mythological approach of the Pythagoreans which promoted a multi-dimensional number theory.
Only after Riemann's multi-dimensional geometry and, finaly, by the Limitation Theorems of Kurt Godel, this belief system was radically questioned.
Interestingly, in the 20th century China developed important work for automatic proof systems for geometry. While the West was more interested in automatic proof systems for logical systems.
Art of Calculation
(2). "Chinese mathematical tradition is algorithmic." Steve Han
Chinese mathematics, was defined by Chinese in ancient times as the "art of calculation" (suan chu). This art was both a practical and spiritual one, and covered a wide range of subjects from religion and astronomy to water control and administration.
http://www.crystalinks.com/chinamath.html
In the West we are taught that the real difference between mathematics as an art of calculation and as a science started with the Greek mathematicians which contemplated numeric attributes not recognized by Babylonian-Egyptian mathematics, which remained on the level of an art&craft.; Only with such an insight, independent on practical interests, like at first, into the difference of even and odd numbers and their attributes for further manipulations, mathematics as a scientific theory was established.
But a first glance at the Lo Shu shows, that the distinction of even and odd numbers was recognized and used for practical and theoretical reasons long before.
The Metaphor of Lo Shu
The Lo Shu Story is very interesting! I think it supports very much my ideas about the relationship of Chinese writing (logograms) and the design of new mathematics, maybe based on Morphogrammatics.
The metaphor of Lo Shu seems to confirm that Chinese math is radically different from Greek math as we know it in Western mathematics.
1. First it is in a written form, thus it has to be read (and not heard), i.e., it has to be deciphered and this knowledge has to be translated into sentences, i.e., into spoken language and then interpreted.
2. This procedure is not happening to a single Genius, like a Eureka insight, happening in the mind and then translated into spoken language and from there to an inscribed and written form. What happens with Lo Shu is a societal, co-operative and negotiating interpretation of the inscription on the back of the turtle which has to be discovered.
2. It is practical. The calculation which happens after the "child", i.e., a member of the population, not a Genius, discovered the signs on the turtle, i.e., the magic square, is practical (and mythical, sacrifice for the river-god) bridging the gap between culture and nature to stop the flooding.
3. Thus, the sign on the turtle is in fact not a sign but a topological logogram (morphogram), a tabular matrix, a mathematical inscription. But there is no need to identify such a tabular inscribtion with the modern mathematical concept of a matrix.
4. The problem inscribed on the turtle is purely combinatorial, and not in any sense logical, or sentence-based. It is in this sense not a riddle. Also not pronounced by an Oracle, offered to the scholars to interpretation.
5. The "truth" of the Square is given by a the reading (collecting) of it from all possible points of view, i.e., from all positions of the counting process, the sum has to be the same, which is 15. This process is generating an invariance principle as the form of truth.
6. The way of the counting, represented by the chain of numbers, is for all positions different. Each point of view has its own history and rationality.
7. The final result, the number 15, is not depending on the view-points, but is invariant of the single approaches. It is producing a collective mediation of the different positions, and at once generating societal collectivity. Also it appears as a final result, 15, the number is complex by the history of its construction. Each position has its own number 15. But a single result wouldn't convince the river-god. The convincing result is the collective number 15 as a result of mediation.
8. To each position, point of view, a singular number system can be attributed. Thus the result can be seen as a mediation, harmony, of different number systems. There is no information involved which would demand a unique number system like the modern linear arithmetic of natural numbers.
9. Also it is connected with numbers, the numbers are placed in a tabular order, square, grid, matrix and not linearly as a singular succession. The numbers are marked as patterns. Despite the strict positionality of the numbers, there is no zero sign involved.
There are many more interesting aspects in the story, like the fact that the turtle-matrix gives access to Nature. Thus, the writing is a bridge between human culture and nature. The turtle is considered as celestial. It is also producing time, societal time of the people involved. It is local, a gift for the specific river-god, but connected with a global cosmic insight. The Lo Shu is mediating local and global thematizations.
With this grammatological approach, I tried to avoid to map the Magic Square of Lo Shu to Western binary digitalism and arithmetic as it is usual today. Thus, in strict mathematical terms, the Lo Shu is not a Magic Square. Simply because it is not a mathematical matrix based on natural numbers. Such an interpretation of Lo Shu as a Magic Square is denying its specific Ancient concept of Numbers. This may have far reaching consequences in the context of interpretations of I Ching, Trigrams, Feng Shui and Yin&Yang.;
Chinese culture: Constructivism
Constructivism, in the West, is based on mathematical constructivism in the sense of Brouwer and Heyting. It is totally different from the Chines Constructivism as suggested by the Turtle Metaphor. Western constructivism is based on a solitaire, mental, subjective insight in the nature of Numbers. It is based on subjective intuition. Only later, as a second step, the intuitions have to be written down; down from the mind to the paper. Today, to a computer program.
Therefore, Western constructivism lacks all the characteristics mentioned above: written, societal, negotiable, practical, combinatorial, tabular, dynamic, etc.
Constructivism in Western philosophy and cybernetics (Second-Order Cybernetics) is more speculative, involving some circularities, but is nevertheless very close to mathematical constructivism (intuitionism) and its problems with solipsism.
Constructivism, today, is very much supported by the needs of computer science.
http://hanxianping.blogchina.com/886414.html
Magic Square in Lo Shu
(1)."Magic Square occurred in Lo Shu of the ancient China.
I think that represents the core of Chinese culture: Constructivism, Combinatorics. But they never become main stream culture in China." Steve Han
The story of 'Lo Shu' is as follows:
In the ancient time of China, there was a huge flood.
The people tried to offer some sacrifice to the 'river god'
of one of the flooding rivers, the 'Lo' river, to calm his
anger. However, every time a turtle came from the river and
walked around the sacrifice. The river god didn't accept
the sacrifice until one time, a child noticed the curious
figure on the turtle shell. Hence they realized the correct
amount of sacrifice to make.

http://mathforum.org/alejandre/magic.square/loshu.html
Legends attribute China prehistoric personality, Hsia Yu () - he who tamed the Yellow River of floods ( ) to be the one who discovered the Lo Shu.Lo Shu, "scroll of the river Lo", dating as early as 2800 BC.
Yu saw some very interesting markings on the shell of a giant tortoise that emerged from the River Lo in Central China. This became Lo Shu.
http://www.hiakz.com/loshu.asp
In Chinese, the square is known as Luo Shu (Simplified Chinese: 洛书; Traditional Chinese: 洛書; pinyin: luò shū; Literal: Luo (River) Book) or the Nine Halls Diagram (Simplified Chinese: 九宫图; Traditional Chinese: 九宮圖; pinyin: jiǔ gōng tú).
http://en.wikipedia.org/wiki/Lo_Shu_Square
Magic Square
A magic square is a square array of numbers consisting of the distinct positive integers 1, 2, ..., n^2 arranged such that the sum of the n numbers in any horizontal, vertical, or main diagonal line is always the same number (Kraitchik 1952, p. 142; Andrews 1960, p. 1; Gardner 1961, p. 130; Madachy 1979).
Lo Shu is an associative magic square, but not a panmagic square.
(enter: Latin Square, Panmagic Square, associative Magic Square)

http://mathworld.wolfram.com/MagicSquare.html
Chinese vs. Greek mathematics
The first thing to understand about ancient Chinese mathematics is the way in which it differs from Greek mathematics. Unlike Greek mathematics there is no axiomatic development of mathematics. The Chinese concept of mathematical proof is radically different from that of the Greeks, yet one must not in any sense think less of it because of this. Rather one must marvel at the Chinese approach to mathematics and the results to which it led.
Chinese mathematics was, like their language, very concise. It was very much problem based, motivated by problems of the calendar, trade, land measurement, architecture, government records and taxes. By the fourth century BC counting boards were used for calculating, which effectively meant that a decimal place valued number system was in use. It is worth noting that counting boards are uniquely Chinese, and do not appear to have been used by any other civilization.
http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Chinese_overview.html
Axiomatic Method
Chinese mathematicians didn't develop axiomatic methods like the Euclidean axioms of geometry. It seems, that this, too, was based on a clear decision and not on a lack of mathematizing ingenuity. Chinese mathematicians had been introduced to Euclid by Westerners. They liked the concise presentation of the topics but didn't think to adopt it to their own methods.
The axiomatic method, as developed by Euclid, is based on the evidence into the "eternal" truth of the axioms and the uniqueness of the rules of deduction. Aristotle has given in his Metaphysics a decisive philosophical justification of this world-view. He defended it against the more mythological approach of the Pythagoreans which promoted a multi-dimensional number theory.
Only after Riemann's multi-dimensional geometry and, finaly, by the Limitation Theorems of Kurt Godel, this belief system was radically questioned.
Interestingly, in the 20th century China developed important work for automatic proof systems for geometry. While the West was more interested in automatic proof systems for logical systems.
Art of Calculation
(2). "Chinese mathematical tradition is algorithmic." Steve Han
Chinese mathematics, was defined by Chinese in ancient times as the "art of calculation" (suan chu). This art was both a practical and spiritual one, and covered a wide range of subjects from religion and astronomy to water control and administration.
http://www.crystalinks.com/chinamath.html
In the West we are taught that the real difference between mathematics as an art of calculation and as a science started with the Greek mathematicians which contemplated numeric attributes not recognized by Babylonian-Egyptian mathematics, which remained on the level of an art&craft.; Only with such an insight, independent on practical interests, like at first, into the difference of even and odd numbers and their attributes for further manipulations, mathematics as a scientific theory was established.
But a first glance at the Lo Shu shows, that the distinction of even and odd numbers was recognized and used for practical and theoretical reasons long before.
The Metaphor of Lo Shu
The Lo Shu Story is very interesting! I think it supports very much my ideas about the relationship of Chinese writing (logograms) and the design of new mathematics, maybe based on Morphogrammatics.
The metaphor of Lo Shu seems to confirm that Chinese math is radically different from Greek math as we know it in Western mathematics.
1. First it is in a written form, thus it has to be read (and not heard), i.e., it has to be deciphered and this knowledge has to be translated into sentences, i.e., into spoken language and then interpreted.
2. This procedure is not happening to a single Genius, like a Eureka insight, happening in the mind and then translated into spoken language and from there to an inscribed and written form. What happens with Lo Shu is a societal, co-operative and negotiating interpretation of the inscription on the back of the turtle which has to be discovered.
2. It is practical. The calculation which happens after the "child", i.e., a member of the population, not a Genius, discovered the signs on the turtle, i.e., the magic square, is practical (and mythical, sacrifice for the river-god) bridging the gap between culture and nature to stop the flooding.
3. Thus, the sign on the turtle is in fact not a sign but a topological logogram (morphogram), a tabular matrix, a mathematical inscription. But there is no need to identify such a tabular inscribtion with the modern mathematical concept of a matrix.
4. The problem inscribed on the turtle is purely combinatorial, and not in any sense logical, or sentence-based. It is in this sense not a riddle. Also not pronounced by an Oracle, offered to the scholars to interpretation.
5. The "truth" of the Square is given by a the reading (collecting) of it from all possible points of view, i.e., from all positions of the counting process, the sum has to be the same, which is 15. This process is generating an invariance principle as the form of truth.
6. The way of the counting, represented by the chain of numbers, is for all positions different. Each point of view has its own history and rationality.
7. The final result, the number 15, is not depending on the view-points, but is invariant of the single approaches. It is producing a collective mediation of the different positions, and at once generating societal collectivity. Also it appears as a final result, 15, the number is complex by the history of its construction. Each position has its own number 15. But a single result wouldn't convince the river-god. The convincing result is the collective number 15 as a result of mediation.
8. To each position, point of view, a singular number system can be attributed. Thus the result can be seen as a mediation, harmony, of different number systems. There is no information involved which would demand a unique number system like the modern linear arithmetic of natural numbers.
9. Also it is connected with numbers, the numbers are placed in a tabular order, square, grid, matrix and not linearly as a singular succession. The numbers are marked as patterns. Despite the strict positionality of the numbers, there is no zero sign involved.
There are many more interesting aspects in the story, like the fact that the turtle-matrix gives access to Nature. Thus, the writing is a bridge between human culture and nature. The turtle is considered as celestial. It is also producing time, societal time of the people involved. It is local, a gift for the specific river-god, but connected with a global cosmic insight. The Lo Shu is mediating local and global thematizations.
With this grammatological approach, I tried to avoid to map the Magic Square of Lo Shu to Western binary digitalism and arithmetic as it is usual today. Thus, in strict mathematical terms, the Lo Shu is not a Magic Square. Simply because it is not a mathematical matrix based on natural numbers. Such an interpretation of Lo Shu as a Magic Square is denying its specific Ancient concept of Numbers. This may have far reaching consequences in the context of interpretations of I Ching, Trigrams, Feng Shui and Yin&Yang.;
Chinese culture: Constructivism
Constructivism, in the West, is based on mathematical constructivism in the sense of Brouwer and Heyting. It is totally different from the Chines Constructivism as suggested by the Turtle Metaphor. Western constructivism is based on a solitaire, mental, subjective insight in the nature of Numbers. It is based on subjective intuition. Only later, as a second step, the intuitions have to be written down; down from the mind to the paper. Today, to a computer program.
Therefore, Western constructivism lacks all the characteristics mentioned above: written, societal, negotiable, practical, combinatorial, tabular, dynamic, etc.
Constructivism in Western philosophy and cybernetics (Second-Order Cybernetics) is more speculative, involving some circularities, but is nevertheless very close to mathematical constructivism (intuitionism) and its problems with solipsism.
Constructivism, today, is very much supported by the needs of computer science.

3 Comments:
在人类文化发展历史上,常有这样的一种效应,在一种文明中发育的文化往往在另外一种文明的民族文化中得到发扬光大;最能理解和最先理解了中国古代文明精髓的恰恰是欧洲人如莱布尼兹!这有点儿像生物界的现象,物种的亲缘关系越远就越容易把优秀的生物性状遗传下去。
H.J.Ryser在他的组合学名著《Combinatorial Mathematics》(1962)中说:“组合数学也称为组合分析或者组合学,是一门起源于古代的数学学科。中国的大禹时代(公元前2200年)在一只神龟的背上看到幻方;而大约公元前1100年,排列组合即已在中国开始萌芽......”。现在组合学这个名称已经固定下来了——Combinatorics;而组合学之对于网络计算机时代,正如欧几里得几何学之对于机器时代。
这里有一个中国传统数学的网上资源:http://elib.lib.tsinghua.edu.cn:9080/mathdl/htm/index.jsp
是清华大学的。中国传统数学一般叫作“中国古算”,正像鲁道夫说的,中国还没有认识到自己文化典籍的真正价值。
Post a Comment
Links to this post:
Create a Link
<< Home