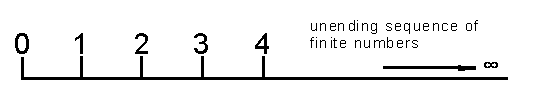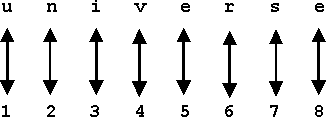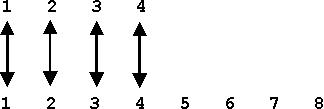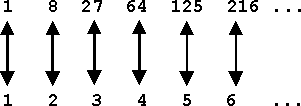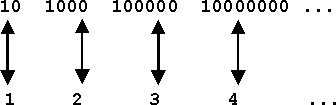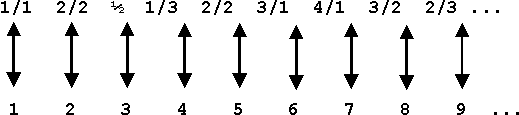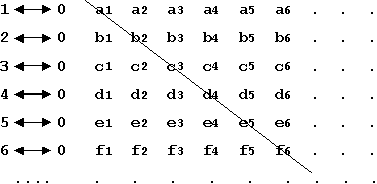|
ACHILLES AND THE TORTOISE |
|||||||||||||||||||||
| This, gentlemen, is a stiff dose of philosophical logic. This is, moreover, a three-part article. But there's one simple reason why this magazine should carry it; it is a rigorously logical attack on the problem of inter-stellar flight. It is an integrated attack on the problem of what that fine old "space-warp" or "hyper-space" means in specific physical-science terms. And it starts, necessarily, with the ancient question "What is motion?" If we are to escape Relativity limitations, we must start at a more fundamental level, not build up from Relativity. | |||||||||||||||||||||
- part 1 of 3 - |
|||||||||||||||||||||
| by GOTTHARD GÜNTHER | |||||||||||||||||||||
It is probable that the problem of interplanetary space travel may be solved in scientific and technical terms with which we are already familiar. But the situation looks very different when we approach the question of interstellar or even intergalactic voyages. The distances involved are so gigantic that interplanetary methods will be useless, and so will be the logical and physical concepts on which they are based. The following article tries to present some novel concepts - implied by recent developments in mathematics and physical science - which seem to contain the solution to the problem how to cross Deep Space. The ideas expressed in this article have grown out of a correspondence between John W. Campbell, Jr. and the author. Although Mr. Campbell has occasionally been referred to in the text, his share in the ideas expressed herein has been much greater. In fact there is hardly any side to the problem in the development of which he did not participate. So what he claims as his own should be recognized as such. The actual presentation, of course, is the exclusive responsibility of the author, and any errors that might have occurred are solely his. |
|||||||||||||||||||||
| So you really know precisely what motion in space means? When you get behind the steering wheel of your car and travel from, let us say, New York City to San Francisco, you know exactly what you do? Well, let us admit that in a practical sort of way you should indeed know what you are doing. If not, then may God help the other road users. It is, however, a very different matter if we ask the question: do we know in exact theoretical and scientific terms what motion in space actually is and how it happens? The answer is a most emphatic No! It may seem strange that something so commonplace, something we do every day as long as we live, involves unsolved logical and scientific problems. But that is the case. It is still a complete mystery to us, what actually happens when a physical body moves from one point in space to some other point. | |||||||||||||||||||||
| There is a reason for it. Nowadays we are finally beginning to know what Matter is, and what basic laws seem to define its ultimate structure. But we have not the slightest idea what Space - the mere absence of anything "physical" - might mean. It stands to reason: as long as we cannot give even an approximate meaning to the general term "Space", it will be absolutely impossible to have even the haziest concept about what really does happen when a body moves in space from one point to another. If we try to explain it, we get entangled in contradictions and paradoxes - a clear indication that our present thinking methods are inadequate even to pose the problem. | |||||||||||||||||||||
This has been known since the times of ancient Greece, and the most famous exposition of the riddle that is offered by the phenomenon of motion in space is Zeno of Elea´s paradox of Achilles and the Tortoise. Achilles, the fastest runner that ever lived, cannot overtake the Tortoise, the slowest animal. Zeno's argument runs as follows: Let AZ (see diagram across bottom) be the race track. Achilles starts from A, the Tortoise at the same time from B. If we assume that the Homeric hero runs twice as fast as the animal, the inference seems inevitable that both racers should reach point Z at the same time; but such was not Zeno´s conclusion. This famous philosopher argued that while Achilles covers the distance AB, the Tortoise reaches point C. That is halfway between B and Z. When Achilles arrives at C, the animal must have reached D, this time midway between C and D. When Achilles is at D, that Tortoise must have gone to E. When Achilles passes E, the animal is necessarily at F. And when our hero is at F the Tortoise has again passed half the distance between F and Z and is, therefore, now at G, and so ad infinitum. It follows, so Zeno concludes, that Achilles can never overtake the Tortoise. And, incidentally, neither of the runners can ever reach Z. |
|||||||||||||||||||||
 |
|||||||||||||||||||||
The point of the argument is, of course, the influx of Time. Whenever Achilles reaches a designated point it has taken him time to get there from the preceding one, and during this time lapse the Tortoise has moved on to the next - as the animal is in constant motion. And no matter how short the distance will ultimately become, some time must always elapse till Achilles may cover it, and during that time interval the Tortoise shall have moved away from the point the pursuer is about to reach. There is only one possibility that Achilles may catch up with the Tortoise. If the Homeric hero would move with infinite speed and would, therefore, cover the distances between A, B, C, D, ¼ , Z in zero time, then the Tortoise would have no time to get away from point B as soon as the race starts. The beginning of the race and its finish would be the same identical moment. In other words: there would be no race at all. But if there is a race - with finite speeds for the racers - no overtaking could ever take place. We all know from the practical viewpoint of our everyday experience that Zeno's argument is sheer nonsense. But the baffling thing is, although it is contradicted by the commonest actions in everybody's life, Zeno's point is logically unassailable. There is no technical flaw in his reasoning. He has indeed with his paradox touched the very problem of space and its relation to motion, and his argument indicates one of the deepest insights into the metaphysical structure of the world. Alfred North Whitehead once remarked: "I am fond of pointing out to my pupils that to be refuted in every century after you have written is the acme of triumph. I always make that remark in connection with Zeno. No one has ever touched Zeno without refuting him, and every century thinks it worth while to refute him." ("Essays in Science and Philosophy", New York 1947, p.114.) Obviously none of these refutations has ever been final. Zeno's paradox is now more than two thousand years old and the discussion about its merits is still going strong. However, in modern textbooks
on logic and metaphysics the reader may frequently find a
(mistaken) statement to the effect that the infinitesimal
calculus has finally solved Zeno's problem. The argument
usually runs as follows: mathematically speaking the
paradox of motion in space resolves itself into a problem
of limits. If our race track AZ=x, and Achilles' handicap
AB = 1, then obviously we have But Zeno constituted an unending series AB + BC + CD + DE + EF + ¼ with the stipulation that every given distance (except the first) is exactly one half of the preceding one. We, therefore, obtain for x the equation:
The question now is: does the right side of the equation equal 2? If that is the case, then it is mathematically demonstrated that Achilles must overtake the Tortoise at point Z. This is the moment when the concept of "limit" is introduced. It is a device which enables us to circumscribe the infinity of numerical terms which turn up at the right side of our equation for x by a finite operation. The procedure involved was developed by the French mathematician Cauchy (1789-1857), and it shows that the right side of our equation is exactly 2. The "trick" of Cauchy's technique is, of course, that he eliminates the Infinite, because we cannot think it, and replaces it with the notion "limit." This substitute term permits a rigorous mathematical treatment /1/ and produces a "solution" for Zeno's paradox. Now let us have a closer look at the "solution". What does it really demonstrate? It proves in the most rigorous way that our common sense experience, that Achilles does overtake the Tortoise, is right. But we know that anyhow. And no person in his right senses ever doubted it. Not even Zeno himself! When he developed his famous paradox he meant something very different. Explaining it to his disciples he might have said: There is a trivial and everyday occurrence like motion in space. It is absolutely convincing to our senses, and nobody doubts its existence. Yet at the same time that trivial fact defies any attempt to think it in noncontradictory terms. The phenomenon of motion as such is positively unthinkable. And it is unthinkable because the concept of Infinity is involved. Think Infinity and you will have solved my paradox. But there is the rub: Infinity is unthinkable for human thought. This shows us that the solution provided by modern calculus is no genuine logical solution. It detours the real difficulty, the problem of the Infinite, and replaces it by a different concept, the limit, which corresponds to our normal practical experience. It detours the real difficulty, the problem of Infinite, and replaces it by a different concept, the limit, which corresponds to our normal practical experiences. It does not show us how to think the element of Infinity involved in the mystery of motion. It does exactly the opposite: it shows us how to avoid it. Zeno's original problem: what is it that creates an apparently insolvable paradox in our consciousness if we try to think "motion", has not been solved by the technique of calculus. This has been borne out by the history of calculus itself. Its first discoverers, Newton and Leibniz, tried very hard to exclude the concept of an infinitely small quantity from their mathematical procedures. However, they did not fully succeed. The validity of their methods was doubted, and the technique of calculus did not attain its full scientific rigor till the notion of Infinity was finally eliminated, and replaced by the more modest concept of "limit". The calculus was recognized to be incompetent to deal with problems of genuine Infinity and the very essence of Zeno's paradox remained unsolved /2/. "So what?" the reader might ask. "Isn't it enough that we have a mathematical tool that can compute any sort of motion we might observe in Space? Computation is sufficient for all practical purposes. So why bother about mysterious metaphysical properties of Space, Time and Motion !" I am sorry, but it is not as simple as all that. First, our computation methods are already insufficient, when we encounter a so-called three-body-problem. And then: what about interstellar travel? Existing and computable types of locomotion may be satisfactory for travel on this planet and even in interplanetary space. But they are decidedly unsatisfactory when it comes to bridging interstellar distances within reasonable time intervals. As long as we don't know anything about the structural properties of the so-called "continua" -Space per se is a "continuum" and so is Time - we cannot even ask the question whether these as yet unknown properties might permit types of locomotion, as yet equally unknown, by which a body (a spaceship) might alter its own position in space. The idea of a "space warp", so frequently encountered in science fiction points in that direction. If something like it existed, it would be a "motion" measured in terms of something other than distance - or time-units. The only way to discover and explore physical possibilities that might lie in this direction is the analysis of the paradox properties of the Space- and Time-continuum. And these properties are structural characteristics of the Infinite. Therefore Zeno should be very much alive with us. It is obvious that the failure to make Zeno's problem disappear was the failure of mathematics to develop a method to deal with the Infinite. The Infinite was just the limit of our numerical conceptions. We could approach, but never reach it, and within its realm all operational procedures broke down. Infinite plus one was Infinite. Infinite plus a million was Infinite, and Infinite plus Infinite still was nothing but Infinite. In other words: Infinite was the absolute limit for the counting process and, therefore, the limit-concept of quantity in general. This was what children learned in school, and it was also the limit of wisdom for the accomplished mathematician. All this was changed, overnight so to speak, by the work of one man who ranks equal with the greatest in the history of mathematics. His name was Georg Cantor (1845-1918). He was born in Russia, lived the greater part of his life in Germany, and died as professor of mathematics at the University of Halle (Germany). During the final quarter of the last century Cantor published a series of articles which completely revolutionized our concept of number, of counting, and generally of quantity. In these articles Cantor transcended the concept of limit, thus ultimately bringing the very concept of Infinity within the grasp of mathematical technique. Cantor's results are so startling, nay, so unbelievable and fantastic for the normal mind that they were first attacked by mathematicians from every quarter. Today they are basically accepted, and they have led to a most radical overhauling of the foundations of traditional logic as well as classical mathematics. What Cantor has discovered can be summarized by the following statement: We are in error if we assume that the process of counting is limited by the concept of the Infinite - and that Infinite itself has no definite quantitative properties. It is, on the contrary, possible to count beyond Infinite and to construct an unending series of numbers, the smallest of which is our traditional concept of Infinite. Any subsequent number in this series is of higher arithmetical magnitude than mere Infinite. Cantor called these numbers which are of higher numerical power than the mere limit-concept of Infinite the transfinite numbers, or transfinite sets. |
|||||||||||||||||||||
In other words: Cantor distinguishes two structurally - different types of numbers. The first group are our familiar numbers which designate finite objects and relations. Finite realm of counting:
The second group comprises the Transfinite realm of counting:
In order to designate these transfinite numbers Cantor used the first letter of the Hebrew alphabet, Aleph, with a numerical index. His numbers are, therefore, called the Aleph-numbers, or short: the Alephs. They begin, as our figure shows, with À 0, or Aleph zero (sometimes called Aleph naught), which is the completed traditional Infinite, and ascend from there to higher and higher numerical powers of the Transfinite and finally converge against a transfinite limit Á i /3/. In order to understand the fantastic orders of magnitude which are implied in the transfinite realm of counting one should realize that, if À 0 is the completed traditional order of Infinite, then À 1 is a number which represents the infinite power to the traditional infinite. Now, if a mathematician makes the unheard of claim that he has discovered a new type of number series by dint of which he can determine differences of magnitude within the Infinite he is, of course, under obligation to explain how his new concept of number differs from our familiar finite numbers. Cantor's explanation is very simple and can be understood without any specific mathematical training. We have to make only a few preliminary steps. First we ask, what, do we do when we count? The answer is: we establish a one-to-one correspondence between a group of objects and a second group of numerical concepts. Let us, for instance, count the letters in the word "universe":
Our double-headed arrows indicate the one-to-one correspondence between letter and number, and we see that the cardinal number which determines the quantity of letters used in "universe" is eight. In other words "8" represents a set of integers which is equivalent to the number of letters in our word. Of course it is obvious, if we call "8" a set of integers, then "1", "2", "3", "4", ¼ , are sub-sets of our original set. And as we have counted letters or could count apples, horses, cars or ideas, we might as well count any such sub-set. Let us take for instance the sub-set "4" and count it with our original set:
Everybody can see that the result is not a one-to-one correspondence between our counting numbers (below) and our counted objects (set "4"), but a one-to-two correspondence. There is no equivalence between our counting numbers and the counted set. We discover here the basic logical characteristic of all finite numbers which can be expressed as follows: No finite number set is equivalent to a proper sub-set of itself. This maxim holds unconditionally for the finite realm of counting and its application tells us that a certain number in question is finite. But what is obvious for the Finite is false for the Infinite! In order to understand what follows, please let me remind you that the numerical magnitude of a counted set is always established by a one-to-one correspondence with a counting set - as it was the case with the letters of "universe" and the set "8." Now turning to infinite sets it would seem that the set of all positive integers (even and odd) should be of higher numerical magnitude than the set of all even numbers. We again apply our system of pairing the counted (above) and the counting numbers:
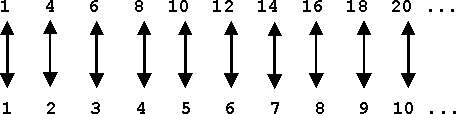
No matter how long we continue our pairing - and we assume it to be an unending series - we shall never run out of counting numbers, but we shall also never exhaust the series of even numbers which we want to count. Of course, the class of even integers is "thinned out" as compared with the class of all integers, but this, "thinning out" has not the slightest effect on the order of numerical magnitude for the "thinned out" series. Such is the nature of even the lowest form of infinity! To drive this most important point home I shall give you two more examples, of such "thinning out" processes and their one-to-one correspondence with our unending series of integers:
The counted series in this case are the cubes (13, 23, 33, ¼ ) of the integers - and again we shall never run out of counted numbers as little as of counting integers. Both series are of equal numerical magnitude, because both converge against the same infinite limit. As our last example we might finally stipulate that only such numbers shall be counted which begin with a "1", an odd number of zeros following:
No matter how radical our "thinning out" process is, the unending series above our double-headed arrows can never be exhausted by our counting integers. In other words, there are "as many" numbers in the series 10, 1000, 100000, ¼ , as there are in 1, 2, 3, ¼ This seems to be the height of absurdity, but it is the inevitable logical consequence of the process we applied when we counted the letters in the word "universe". It is now possible to state exactly what we mean if we call a set of numbers infinite. We defined a finite set as one which is not equivalent to a proper sub-set of itself. And we now say: Any set that is equivalent to a proper sub-set of itself is infinite. And this Infinite is the first number of Cantor´s set of transfinite Alephs. It is the À 0 of the transfinite realm of counting. The next problem, of course, is how to proceed to our next transfinite number which should be "bigger" than our traditional Infinite. It is not too difficult to do so. Before we even begin to construct the next transfinite Aleph we can deduce what basic logical property it should have. The following table of properties, common and not-common to finite and infinite sets, should help: |
|||||||||||||||||||||
This table shows the logical situation at one single look. Finite and infinite sets differ as to their equivalence characteristics, but they are both denumerable. That means, there is always a method of counting the members of the different sets. And the method is the same. It stands to reason, if we want to find a third type of numerical set which differs from the finite as well as the infinite, this third type will have to negate what is common to its predecessors. To word it positively, the next transfinite number will have to be non-denumerable. To obtain an expression for a non-denumarable Aleph let us do some transfinite arithmetic. It bears, as you will see, very little resemblance to that of the finite numbers:
(where n represents any finite number)
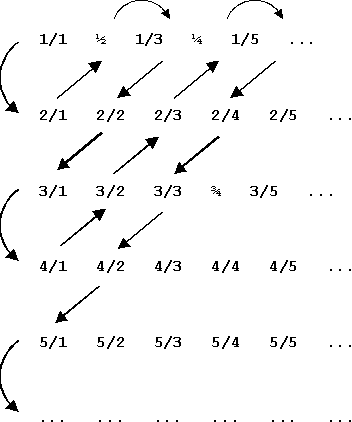
There seems to be no variation in the result of these operations, but it is all very deceptive and treacherous. Because the result is quite different when we try: (À 0)À 0 This equation creates a new transfinite number of higher numerical magnitude than the first number of Cantor´s series. This second Aleph number is non-denumerable. But what does non-denumerability actually mean? We shall find out by following some of Cantor´s trends of thought. Common sense tells us that there are more fractions than integers; for in between any two integers there is an infinite number of fractions. Alas - common sense is amidst alien corn in the land of the Infinite. Although the rational fractions have no definite neighbors Cantor discovered a simple but elegant method to count them, thus proving their denumerability. He arranged the set of all rational fractions not in order of increasing magnitude (that is impossible) but in order of ascending numerators and denominators in the following array:
Now the familiar one-to-one correspondence with the integers - necessary for the process of counting - may be effected.
It follows, the number of all rational fractions is denumerable, hence also of the order of magnitude of À 0. It may be hard to believe that there are "only" as many rational fractions as there are integers, especially in view of the fact that there are an infinite number of fractions between any two integers, but such are the mathematics of the infinite. Even with adding all rational fractions to our previous concept of À 0 we have not yet left the arithmetical dimension of denumerability. However, Cantor's greatest triumph came when he could show that the class of rational plus irrational numbers - i.e. of the so-called real numbers - is of a higher order of magnitude than the denumerable À 0. The class of real numbers is non-denumerable. His proof is based on a reductio ad absurdum. He assumed that the real numbers between 0 and 1 were countable and could be paired with the integers. All real numbers can be expressed as non-terminating decimals, and Cantor wrote them down in the following array for counting:
If this array (where a1, a2, ¼ ; b1, b2, ¼ ; et cetera, are ciphers of the series 0, 1, 2, ¼ , 8, 9) is unending in horizontal as well as in vertical direction, it should contain all real numbers and thus be denumerable. But just the opposite is the case. This array exhibits the very contra-diction to the arguments that all sets are denumerable. For, no matter how our non-terminating decimals are actually arranged, it is always possible to find an infinity of other decimals which are not present in the array ¼ although the same is infinite. The question is: how can we determine such omitted decimals? One might argue: as this set-up is unending and we can actually count only a finite number of individual decimals, the ones we claim to be omitted might still turn up in the as yet uncounted infinite reaches of our array. Cantor countered this argument by the discovery of his famous "diagonal procedure". This technique permits us to show that there are real numbers which are not represented in our arrangement. Please take another look at the array of the, decimals. You will find that the ciphers a1, b2, c3, d4, e5, f6, ¼ , are connected by a diagonal line. If we now construct a second decimal fraction (with Greek letters): a 1, b 2, g 3, d 4, e 5, j 6, ¼ , where a 1 differs from a1, b 2 differs from b2, g 3 differs from c3 and so on, then this new number differs from all the unending decimal fractions in our original set in just one place. It differs from the first number in our table in the first place, from the second number in the second place, from the third number in the third place and generally from any n-th number in the n-th place - no matter how far toward the Infinite we may place n. It is, therefore, impossible that our "diagonal number" may turn up in the as yet unexplored reaches of our array. The diagonal number is, therefore, a real number between 0 and 1 not contained in our denumerable array. It is further possible to repeat this procedure an infinite number of times by starting with a2, a3, a4, ¼ or b1, c1, d1, ¼ thus creating not only one but an infinite series of "diagonal numbers". It is herewith demonstrated that the set of all real numbers between 0 and 1 is non-denumerable and, therefore, of higher arithmetical magnitude than the denumerable Infinite. And since the same can be demonstrated for the set of all real numbers between 1 and 2, between 2 and 3, between 3 and 4, and so forth, it follows that the set of all real numbers is also non-denumerable. If this is the case, we must for the first time in the history of human thinking admit logical distinctions within the realm of the Infinite. Because at least two different types of the Infinite have been determined: the denumerable order of the Infinite and the non-denumerable order which is of higher arithmetical power. As the set of the real numbers designates the so-called continuum, Cantor called the transfinite number which represents this set: the transfinite cardinal number c. By some further proof Cantor could show that the cardinal number of all univocal real functions, f, is even of higher transfinite order than c. Thus we already possess three Alephs. The Aleph of the classical Infinite which produced Zeno's paradox, the Aleph of the continuum and the Aleph of the univocal real functions. The arithmetic of c is very much the same as that of À 0. It is interesting and significant that when c is combined with À 0 it swallows the latter completely. Thus we have: /4/
Even the following equation holds:
But the result is different in the next case:
We pointed out before that the number of transfinite Alephs is infinite. Thus f is by no means the highest numerical concept we may conceive. We do know that there exists an unending series of higher Alephs that converges towards ''Campbell's limit", because it can be proven that the set S of the sub-classes of any given class C always possesses a higher cardinal number than C. That means in the case of our number f that the set of its sub-sets is of higher transfinite order than f itself. /5/ This process can be continued ad infinitum. So much about Cantor's daring creation. The next installment of my article will show that Cantor's theory of the transfinite cardinal number c, the Aleph of the continuum, provides a genuine solution to Zeno's paradox. More than that, Cantor's deductions provide an access to an entirely new concept of Space and to a mathematical basis for interstellar space travel. Some of the conclusions about the structural properties of Space, Time and Matter to be drawn from the theory of the Alephs are so startling and so absolutely beyond our present thinking habits that I cannot resist the temptation to finish this article with the statement, that interstellar travel will be possible the very day Achilles really overtakes the Tortoise. So far he does so only within an independent context of Nature - and against the anguished protest of our too limited powers of thinking. But the day of interstellar space travel will be here when Achilles overtakes the Tortoise in our thoughts as well as in Nature. In other words, when we have unraveled the secret of motion. The two following installments of this article have been written with the intent to bring this day nearer.
Footnotes:
/1/
/2/ Zeno's paradox deals with the notion of the spatial "continuum". And it was finally proved by Weierstrass in his example of a "continuous function" that the limit methods of calculus are insufficient to deal with the problem of actual infinity. (K. Weierstrass, "Erstes Beispiel einer stetigen, nirgends differenzierbaren Funktion", Journal für Mathematik, IX, 1875) /3/ For the idea that there should be an ultra-transfinite limit to all Alephs I am indebted to John W. Campbell. In a letter to me, of July 7, 1953, he calls it the transfinite number of the non-denumerable space of imagination". In deference to his interesting ideas on this subject I have given our symbol for the transfinite limit the Index "i". The symbol Á stands for the second letter of the Hebrew alphabet: Beth. /4/ Aleph naught is usually represented in transfinite arithmetic by the letter, a. Mathematicians are in the habit of writing: c + a = c, etc. I have retained À 0 in order to indicate that the Aleph order of the denumerable Infinite is established but not the transfinite magnitude of c. /5/ The principle
of this transfinite induction can be illustrated by a
very elementary example: Let the set A contain only the
three integers 1,2,3. The cardinal number of our set is
3. However, the sub-sets of A (including the null-class)
are (0), (1), (2), (3), (1,2), (1,3), (2,3), (1,2,3).
Count them and you will find that the cardinal number of
the set S of all the sub-sets is 8.
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||
| vordenker Contact:
[email protected] Copyright © Gotthard Günther 1959 Issued: September 2, 1997 |
|||||||||||||||||||||